Cubes and Dices

Cubes and Dices

Easy Questions
Moderate Questions
Difficult Questions
Cubes and Dices Tutorial

Non Verbal Reasoning

Series
Analogy
Classification
Mirror Images
Water Images
Spotting Out The Embedded Figures
Completion Of Incomplete Pattern
Cubes and Dices
Paper Folding
Paper Cutting
Grouping Of Identical Figures
Construction Of Squares And Triangles
  1. Wooden little cubes each with an edge of one inch are put together to form a solid cube with an edge of three inches. This big cube is then painted red all over the outside. When the big cube is broken-up into the original little ones, how many cubes will be without paint?








  1. View Hint View Answer Discuss in Forum

    As per the given all information in above question , we can say that
    The central cube of middle row will be without paint.

    Correct Option: B

    As per the given all information in above question , we can say that
    The central cube of middle row will be without paint.

  1. If a cube is made using above arrangement which word will be in opposite face of the word one?










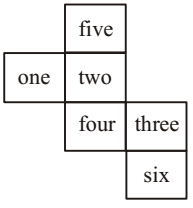
  1. View Hint View Answer Discuss in Forum

    On the basis of following pattern in given open dice , we can say that
    Five will be opposite to Four.
    Similarly , we can find all others words .

    Correct Option: A

    On the basis of following pattern in given open dice , we can say that
    Five will be opposite to Four.
    One will be opposite to Three.
    Two will be opposite to Six.

  1. In a cube using given arrangement, which part be opposite Fruit?










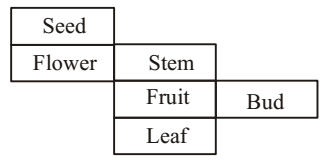
  1. View Hint View Answer Discuss in Forum

    As per the given above open dice , we can see that
    Stem will be opposite of Leaf.

    Correct Option: B

    As per the given above open dice , we can see that
    Stem will be opposite of Leaf.
    Bud will be opposite of Flower.
    Fruit will be opposite of Seed.

  1. If a cube is made using the given arrangements, which color will be opposite the color Green?










  1. View Hint View Answer Discuss in Forum

    We follow the given pattern :-
    From first, second and third figure Orange, Red, Silver and White cannot be on the opposite face of Green colour.

    Correct Option: D

    We follow the given pattern :-
    From first, second and third figure Orange, Red, Silver and White cannot be on the opposite face of Green colour.
    Therefore, Violet is opposite to Green.

  1. The figure below is a drawing of a pile of blocks. When taken apart, how many blocks would be there?










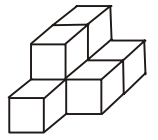
  1. View Hint View Answer Discuss in Forum

    According to question figure , we can say that
    Five block are visible and Two block are invisible.

    Correct Option: C

    According to question figure , we can say that
    Five block are visible and Two block are invisible.
    Hence , Total Number of blocks = 1 + 4 + 2 = 7