11. A compound gear train with gears P, Q, R and S has number of teeth 20,40,15 and 20 respectively. Gears Q and P are mounted on the same shaft as shown in the figure below. The diameter of the gear Q is twice that of the gear R. If the module of the gear R is 2 mm, the centre distance in mm between gears Pand S is
    

1. 1. 40

   
   
   

   2. 80

   
   
   

   3. 120

   
   
   

   4. 160

   
   
   

---

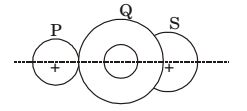
1. View Hint View Answer Discuss in Forum

   m =	D	and mp = mQ
   	T

   
   m_R = m_s for gear meshing condition
   

   Correct Option: B

   m =	D	and mp = mQ
   	T

   
   m_R = m_s for gear meshing condition
   

---

12. The number of degree of freedom of the planetary gear train shown in the figure is
    

1. 1. 0

   
   
   

   2. 1

   
   
   

   3. 2

   
   
   

   4. 3

   
   
   

---

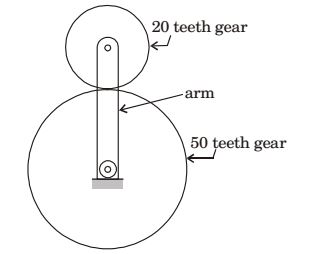
1. View Hint View Answer Discuss in Forum

   A planetary gear train has 2 DOF and hence requires two input to get desired output.

   Correct Option: C

   A planetary gear train has 2 DOF and hence requires two input to get desired output.

---

---

13. A solid disc with radius a is connected to a spring at a point d above the center of the disc. The other end of the spring is fixed to the vertical wall. The disc is free to roll without slipping on the ground. The mass of the disc is M and the spring constant is K. The polar moment of inertia for the disc about its centre is
    

    J =	Ma²
    	2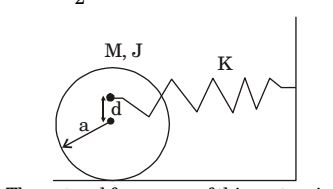

    
    
    The natural frequency of this system in rad/s is given by

1. 1. √	2K(a + d)²
      	3Ma²

   
   
   

   2. √	2K
      	3M

   
   
   

   3. √	2K(a + d)²
      	Ma²

   
   
   

   4. √	K(a + d)²
      	Ma²

   
   
   

---

1. View Hint View Answer Discuss in Forum

   
   

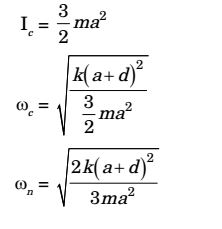
   Correct Option: A

   
   

---

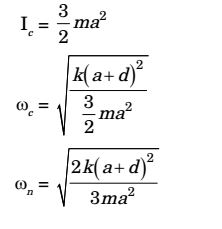
14. The speed of an engine varies from 210 rad/s to 190 rad/s. During cycle the change in kinetic energy is found to be 400 Nm. The inertia of the flywheel in kg-m² is

1. 1. 0.10

   
   
   

   2. 0.20

   
   
   

   3. 0.30

   
   
   

   4. 0.40

   
   
   

---

1. View Hint View Answer Discuss in Forum

   We know, ΔE = Iω²C_S
   Here, ω = 200; ΔE = 400
   

   Cs =	ωmax - ωmin
   	ωmax + ωmin

   
   

   =	20	= 0.1
   	200

   
   ΔE = 400 N – m
   

   ∴ I =	ΔE	=	400	= .10
   	ω²CS		(200)² × 01

   
   

   Correct Option: A

   We know, ΔE = Iω²C_S
   Here, ω = 200; ΔE = 400
   

   Cs =	ωmax - ωmin
   	ωmax + ωmin

   
   

   =	20	= 0.1
   	200

   
   ΔE = 400 N – m
   

   ∴ I =	ΔE	=	400	= .10
   	ω²CS		(200)² × 01

   
   

---

---

15. The torque (in Nm) exerted on the crank shaft of a two stroke engine can be described as T = 10000 + 1000 sin 2θ - 1200 cos 2θ, where θ is the crank angle as measured from inner dead center position. Assuming the resisting torque to be constant, the power (in kW) developed by the engine at 100 rpm is _________.

1. 1. 104.719 kW

   
   
   

   2. 104.59 kW

   
   
   

   3. 105.65 kW

   
   
   

   4. 105 kW

   
   
   

---

1. View Hint View Answer Discuss in Forum

   T = 10000 + 1000 sin2θ – 1200 cos2θ
   N = 100 rpm
   

   ω =	2π × 100	= 10.472 rad/s
   	60

   
   

   Tmean =	1	2π∫0[10000 + 1000sin2θ - 1200 cos2θ]dθ
   	2π

   
   By solving, we get T_mean = 10000 N-m
   

   Power = 10000 ×	2π × 1000
   	60

   
   = 104719.75 W
   = 104.719 kW

   Correct Option: A

   T = 10000 + 1000 sin2θ – 1200 cos2θ
   N = 100 rpm
   

   ω =	2π × 100	= 10.472 rad/s
   	60

   
   

   Tmean =	1	2π∫0[10000 + 1000sin2θ - 1200 cos2θ]dθ
   	2π

   
   By solving, we get T_mean = 10000 N-m
   

   Power = 10000 ×	2π × 1000
   	60

   
   = 104719.75 W
   = 104.719 kW

---