Theory of Machines Miscellaneous
- A rigid link PQ of length 2 m rotates about the pinned end Q with a constant angular acceleration of 12 rad/s². When the angular velocity of the link is 4 rad/s, the magnitude of the resultant acceleration (in m/s²) of the end P is ___________.
-
View Hint View Answer Discuss in Forum

at = Rα = 2 × 12 = 24
aR = ω²R = 16 × 2 = 32
a = √a²t + a²R
= √24² + 32² = 40 m/s².Correct Option: C

at = Rα = 2 × 12 = 24
aR = ω²R = 16 × 2 = 32
a = √a²t + a²R
= √24² + 32² = 40 m/s².
- Match the following with respect to spatial mechanisms.
Type of Joint Degrees of constraint P. Revolute 1. Three Q. Cylindrical 2. Five R. Spherical 3. Four wire 4. Two 5. Zero
-
View Hint View Answer Discuss in Forum
For revolute joint, degree of freedom = 1
For cylinderical joing, degree of freedom = 2
For spherical joint, degree of freedom = 3
Degree of constraints = 6 – Degree of freedomCorrect Option: C
For revolute joint, degree of freedom = 1
For cylinderical joing, degree of freedom = 2
For spherical joint, degree of freedom = 3
Degree of constraints = 6 – Degree of freedom
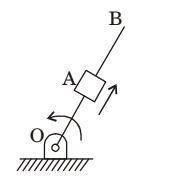
- A link OB is rotating with a constant angular velocity of 2 rad/s in counter clockwise direction and a block is sliding radially outward on it with an uniform velocity of 0.75 m/s with respect to the rod, as shown in the figure below. If OA = 1 m, the magnitude of the absolute acceleration of the block at location A in m/s² is
-
View Hint View Answer Discuss in Forum
αt = 2vω = 2 × 0.75 × 2 = 3
αr = v² = 4; r
a = √a²t + a²r = √3² + 4²
a = 5 m/s²Correct Option: C
αt = 2vω = 2 × 0.75 × 2 = 3
αr = v² = 4; r
a = √a²t + a²r = √3² + 4²
a = 5 m/s²
- The crank of a slider-crank mechanism rotates counter -clock wi se (CCW) with a const ant angular velocity ω, as shown. Assume the length of the crank to be r .
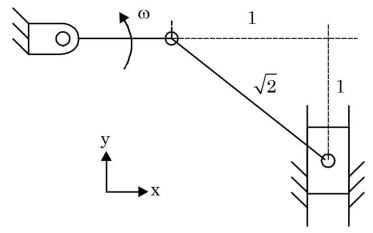
Using exact analysis, the acceleration of the slider in the y-direction, at the instant shown, where the crank is parallel to x-axis, is given by
-
View Hint View Answer Discuss in Forum
Exactly analysis means exact dimensions have to be taken. No approximation is allowed. It means velocity diagram and acceleration diagram with exact geometry (dimensions) need to be drawn.
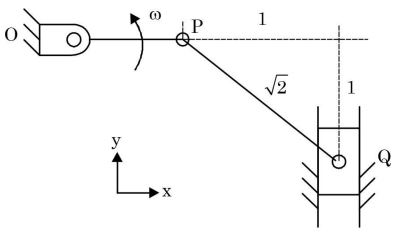
The velocity diagram of the above problem is as follows: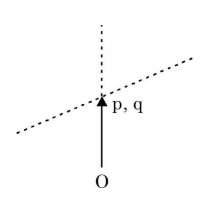
op perpendicular to OP
oq in the direction of movement of slider.
Since, p, q are coinciding i.e. no relative motion between p and q
VP = VQ = rω
and, Vqp = 0 and ωqp = 0
∴ There will be no radial acc. of link PQ.
Only tangential acc.(atqp will be there.
Also for link OP, α = 0 i.e. no tangential acceleration
tan 45° = aq rω
⇒ aq = rω²Correct Option: C
Exactly analysis means exact dimensions have to be taken. No approximation is allowed. It means velocity diagram and acceleration diagram with exact geometry (dimensions) need to be drawn.

The velocity diagram of the above problem is as follows:
op perpendicular to OP
oq in the direction of movement of slider.
Since, p, q are coinciding i.e. no relative motion between p and q
VP = VQ = rω
and, Vqp = 0 and ωqp = 0
∴ There will be no radial acc. of link PQ.
Only tangential acc.(atqp will be there.
Also for link OP, α = 0 i.e. no tangential acceleration
tan 45° = aq rω
⇒ aq = rω²
- A compound gear train with gears P, Q, R and S has number of teeth 20,40,15 and 20 respectively. Gears Q and P are mounted on the same shaft as shown in the figure below. The diameter of the gear Q is twice that of the gear R. If the module of the gear R is 2 mm, the centre distance in mm between gears Pand S is
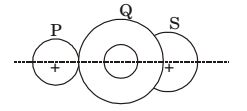
-
View Hint View Answer Discuss in Forum
m = D and mp = mQ T
mR = ms for gear meshing condition
Correct Option: B
m = D and mp = mQ T
mR = ms for gear meshing condition

