Network theory miscellaneous Difficult Questions and Answers | Page - 2

Network theory miscellaneous

The effective resistance between terminals A and B in the circuit shown below is—

1. R
1. R – 1
1. R/2
1. 6 R
  11

View Hint View Answer Discuss in Forum

The given circuit:

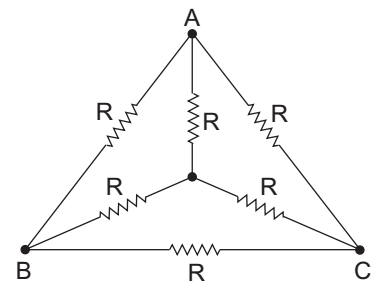
By converting star network into delta network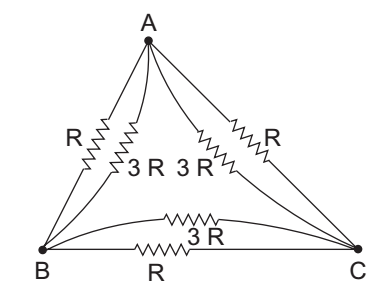

R_{eq. (AB)} = R_AB || (R_AC + R_BC)
Where,
R_AB = R || 3R = 3/4 R
R_AC = R || 3R = 3/4 R
R_BC = R || 3R = 3/4 R
Now,
R_{eq. (AB)} = 3R 3R + 3 R
4 4 4

= 3R 6 R = 3R/4 × 6R/4
4 4 3R/4 + 6R/4

= 18R² = R
16 × (9R/4) 2

Hence alternative (C) is the correct choice.

Correct Option: C

The given circuit:

By converting star network into delta network

R_{eq. (AB)} = R_AB || (R_AC + R_BC)
Where,
R_AB = R || 3R = 3/4 R
R_AC = R || 3R = 3/4 R
R_BC = R || 3R = 3/4 R
Now,
R_{eq. (AB)} = 3R 3R + 3 R
4 4 4

= 3R 6 R = 3R/4 × 6R/4
4 4 3R/4 + 6R/4

= 18R² = R
16 × (9R/4) 2

Hence alternative (C) is the correct choice.

The total power consumed in the circuit shown in the figure is—

1. 10W
1. 12W
1. 16W
1. 20W

View Hint View Answer Discuss in Forum

The given circuit:

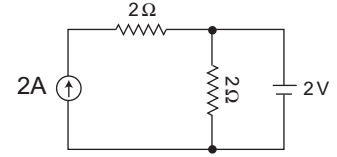
Case 1: When current source is taken:

The net current in branch AB is 2A
Case 2: When voltage source is taken: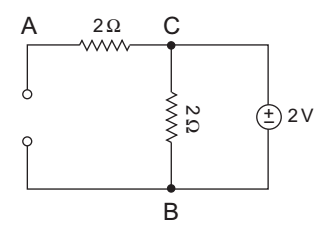

The net current in branch BC is 2/2 = 1A
Now, the total power consumed in the circuit:
= I²_ABR_AB + I²_BC × R_BC
= 2² × 2 + 1² × 2
= 10W.

Correct Option: A

The given circuit:

Case 1: When current source is taken:

The net current in branch AB is 2A
Case 2: When voltage source is taken:

The net current in branch BC is 2/2 = 1A
Now, the total power consumed in the circuit:
= I²_ABR_AB + I²_BC × R_BC
= 2² × 2 + 1² × 2
= 10W.

The time constant of the network shown in figure is—

1. 2RC
1. 3RC
1. RC/2
1. 2 RC
  3

View Hint View Answer Discuss in Forum

The given network:

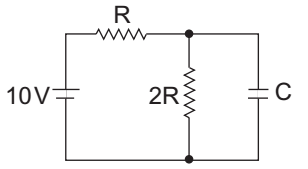
The equivalent circuit for calculating time constant is shown below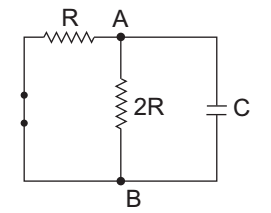

R_eq = R || 2R = 2R
3

Time constant,
τ = R_eq C = 2R . C = 2 RC
3 3

Correct Option: D

The given network:

The equivalent circuit for calculating time constant is shown below

R_eq = R || 2R = 2R
3

Time constant,
τ = R_eq C = 2R . C = 2 RC
3 3

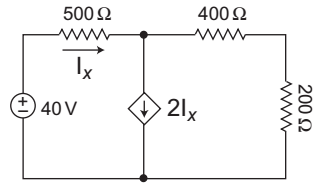
For the circuit shown below, the current I_x and power delivered by the independent source is—

1. 0·4A, 16W
1. – 0·4A, – 16W
1. 4A, 160W
1. – 4A, – 160W

View Hint View Answer Discuss in Forum

The given circuit

Apply KCL at node A
2I_x + V_A –0 = I_x
(400 + 200)Ω

or
I_x = - V_A
600
…(i)
From figure
I_x = 40 - V_A
500
…(ii)
From equation (i) and (ii)
– V_A = 40 – V_A
600 500

or
– 5V_A = 240 – 6V_A
or
V_A = 240V
and
I_x = – V_A = – 240 = – 0·4A
600 600

Power delivered by the independent source is
= 40 × I_x = 40 × (– 0·4) = – 16 W.

Correct Option: B

The given circuit

Apply KCL at node A
2I_x + V_A –0 = I_x
(400 + 200)Ω

or
I_x = - V_A
600
…(i)
From figure
I_x = 40 - V_A
500
…(ii)
From equation (i) and (ii)
– V_A = 40 – V_A
600 500

or
– 5V_A = 240 – 6V_A
or
V_A = 240V
and
I_x = – V_A = – 240 = – 0·4A
600 600

Power delivered by the independent source is
= 40 × I_x = 40 × (– 0·4) = – 16 W.

The circuit shown in figure below is equivalent to a load of—

1. 4 Ω
  3
1. 8 Ω
  3
1. 4Ω
1. 2Ω

View Hint View Answer Discuss in Forum

The given circuit

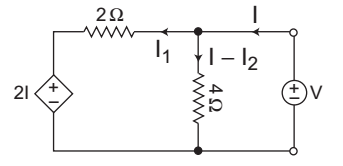
The load is given by ratio of voltage, V to the current, I
V = 4 (I – I₁) …(i)
and
V = 2I₁ + 2I …(ii)
From equation (i) and (ii):
4I – 4I₁ = 2I₁ + 2I
or
2I = 6I₁
or
I = 3I₁
or
I₁ = I/3
Now,
V = 4 I - I = 8I
3 3

or
V = 8 Ω
I 3

Hence alternative (B) is the correct choice.

Correct Option: B

The given circuit

The load is given by ratio of voltage, V to the current, I
V = 4 (I – I₁) …(i)
and
V = 2I₁ + 2I …(ii)
From equation (i) and (ii):
4I – 4I₁ = 2I₁ + 2I
or
2I = 6I₁
or
I = 3I₁
or
I₁ = I/3
Now,
V = 4 I - I = 8I
3 3

or
V = 8 Ω
I 3

Hence alternative (B) is the correct choice.