Network theory miscellaneous Difficult Questions and Answers | Page - 4

Network theory miscellaneous

For the circuit shown below, the value of I₁ = ?

1. 2A
1. 1A
1. 3·6A
1. None of these

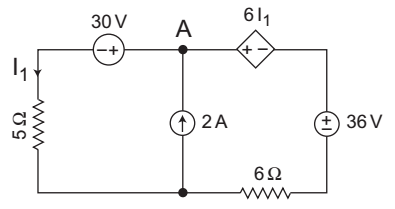
View Hint View Answer Discuss in Forum

The given circuit:

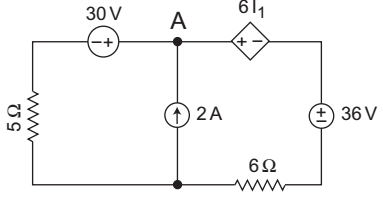
Applying KCL at node A, we get
V_A - 30 + V_A - 36 - 6 l₁ = 2 . . . . . . .(i)
5 6

l₁ = V_A - 30
5

V_A = 5 l₁ + 30 . . . . . . . . . . (ii)
From equation (i) and (ii), we get
V_A 1 + 1 - l₁ = 14
5 6

(5I₁ + 30) 6 + 5 - l₁ = 14
30

or
55 I₁ + 330 – 30 I₁ = 420
or
25 I₁ = 420 – 330 = 90
or
I_{1_{= 90/25 = 18/5 = 3·6
Hence alternative (C) is the correct choice.}}

Correct Option: C

The given circuit:

Applying KCL at node A, we get
V_A - 30 + V_A - 36 - 6 l₁ = 2 . . . . . . .(i)
5 6

l₁ = V_A - 30
5

V_A = 5 l₁ + 30 . . . . . . . . . . (ii)
From equation (i) and (ii), we get
V_A 1 + 1 - l₁ = 14
5 6

(5I₁ + 30) 6 + 5 - l₁ = 14
30

or
55 I₁ + 330 – 30 I₁ = 420
or
25 I₁ = 420 – 330 = 90
or
I_{1_{= 90/25 = 18/5 = 3·6
Hence alternative (C) is the correct choice.}}

If a resistance R of 1Ω is connected across the terminals AB as shown in the given figure then the current flowing through R will be—

1. 1A
1. 0·5A
1. 0·25A
1. 0·125A

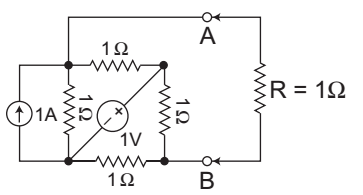
View Hint View Answer Discuss in Forum

The given circuit

Given, R_L = R = 1Ω
Equivalent circuit for calculation of R_th is shown below: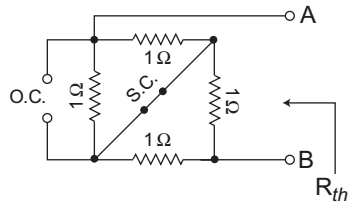

From figure, R_th = (1|| 1) + (1||1) = 1/2 + 1/2 = 1Ω
Equivalent circuit for calculation of Vth is shown below:

Applying KVL in the loop 1, we get
– I₁ × 1 + 1 – I₁ × 1 – 1 = 0
or
I₁ = 0
Again, applying KVL in the loop 2, we get
1 – I₂ × 1 – I₂ × 1=0
or
I₂ = 1/2 A
Now, V_th = 1 × I₁ + 1 × I₂ = 1 × 0 + 1 × 1/2 = 1/2 V
Now,
I₂ = V_th 6 + 5 = 0.5 = 0.5 = 0.25A
R_th + R_L 1 + 1 2

Hence alternative (C) is the correct choice.

Correct Option: C

The given circuit

Given, R_L = R = 1Ω
Equivalent circuit for calculation of R_th is shown below:

From figure, R_th = (1|| 1) + (1||1) = 1/2 + 1/2 = 1Ω
Equivalent circuit for calculation of Vth is shown below:

Applying KVL in the loop 1, we get
– I₁ × 1 + 1 – I₁ × 1 – 1 = 0
or
I₁ = 0
Again, applying KVL in the loop 2, we get
1 – I₂ × 1 – I₂ × 1=0
or
I₂ = 1/2 A
Now, V_th = 1 × I₁ + 1 × I₂ = 1 × 0 + 1 × 1/2 = 1/2 V
Now,
I₂ = V_th 6 + 5 = 0.5 = 0.5 = 0.25A
R_th + R_L 1 + 1 2

Hence alternative (C) is the correct choice.

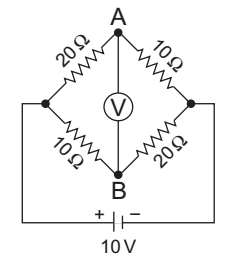
The reading of high impedance voltmeter V in the bridge circuit shown in the given figure—

1. Zero
1. 3·33V
1. 4·20V
1. 6·66V

View Hint View Answer Discuss in Forum

The given circuit:

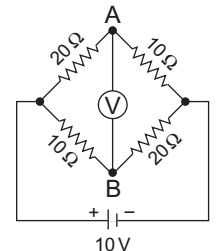
Voltage at terminal A
V_A = 10 × 10 = 10 V
10 + 20 3

Voltage at terminal B
V_B = 10 × 20 = 20 V
20 + 10 3

Now,
V_BA = reading of voltmeter
= 20 = 10 = 10 = 3.33V
3 3 3

Correct Option: B

The given circuit:

Voltage at terminal A
V_A = 10 × 10 = 10 V
10 + 20 3

Voltage at terminal B
V_B = 10 × 20 = 20 V
20 + 10 3

Now,
V_BA = reading of voltmeter
= 20 = 10 = 10 = 3.33V
3 3 3

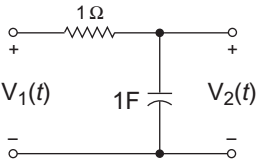
For the following circuit, a source of V₁(t) = e_{– 2t} is applied. What will be the V₂ (t)—

1. 2e_–2t– e_–t
1. e_{– t}
1. e_{– t} – e–2t
1. e_–2t
  2

View Hint View Answer Discuss in Forum

The given circuit

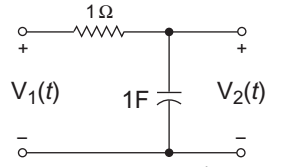
From figure
V₂(s) = V₁(s) 1 = V₁(s)
s
1 + 1
s

= V₁(s) s
(1 + s)

where,
= V₁(s) 1
s + 2

[Given V₁(t) = e^–2t]
Now,
V₂ (s) = 1 × s = A + B
(s + 2) (s + 1) s + 1 s + 2

= - 1 + 2
s + 1 s + 2

or
V₂(t) = 2e^–2t – e^–t
Hence alternative (A) is the correct choice.

Correct Option: A

The given circuit

From figure
V₂(s) = V₁(s) 1 = V₁(s)
s
1 + 1
s

= V₁(s) s
(1 + s)

where,
= V₁(s) 1
s + 2

[Given V₁(t) = e^–2t]
Now,
V₂ (s) = 1 × s = A + B
(s + 2) (s + 1) s + 1 s + 2

= - 1 + 2
s + 1 s + 2

or
V₂(t) = 2e^–2t – e^–t
Hence alternative (A) is the correct choice.

For the circuit shown below, if the power dissipated in the 6Ω resistor is zero then V is—

1. 20√2 ∠ 45°
1. 20 ∠ 30°
1. 20 ∠ 45°
1. 20√2 ∠ 30°

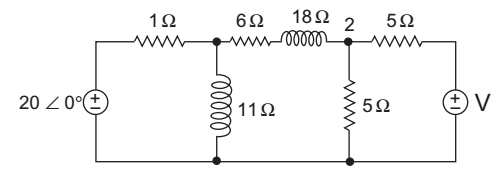
View Hint View Answer Discuss in Forum

The given circuit:

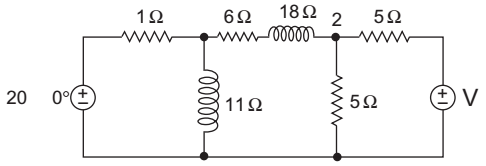
Given that power dissipated in the 6Ω resistor is zero, it means voltage at node 1 is same as 2 (i.e., V₁ = V₂)
KCL at node 1
V₁ - 20    0° + V₁ + V₁ + V₂ = 0
1 j1 6 + j8

or
V₁ 1 + 1 20 0°(since V₁ = V₂)
j1

or
V₁ = 20   0° j .........…(i)
(j + 1)

Again KCL at node 2:
V₂ – V₁ + V₁ + V₂ – V = 0
6 + j8 5 5

or
2V₂ = V (since V₁ = V₂)
5 5

or
V₂ = V ...........(ii)
2

From equation (i) and (ii)
20   0° j = V
j + 1 2

or
V = 2 × 20 0° × 90°
2 × 45°

20 2 45°
Hence alternative (A) is the correct choice.

Correct Option: C

The given circuit:

Given that power dissipated in the 6Ω resistor is zero, it means voltage at node 1 is same as 2 (i.e., V₁ = V₂)
KCL at node 1
V₁ - 20    0° + V₁ + V₁ + V₂ = 0
1 j1 6 + j8

or
V₁ 1 + 1 20 0°(since V₁ = V₂)
j1

or
V₁ = 20   0° j .........…(i)
(j + 1)

Again KCL at node 2:
V₂ – V₁ + V₁ + V₂ – V = 0
6 + j8 5 5

or
2V₂ = V (since V₁ = V₂)
5 5

or
V₂ = V ...........(ii)
2

From equation (i) and (ii)
20   0° j = V
j + 1 2

or
V = 2 × 20 0° × 90°
2 × 45°

20 2 45°
Hence alternative (A) is the correct choice.