1. An electron in hydrogen atom makes a transition n₁ → n₂ where n₁ and n₂ are principal quantum numbers of the two states. Assuming Bohr’s model to be valid the time period of the electron in the initial state is eight times that in the final state. The possible values of n₁ and n₂ are

1. 1. n₁ = 4 and n₂ = 2 ​

   
   
   

   2. n₁ = 6 and n₂ = 2

   
   
   

   3. n₁ = 8 and n₂ = 1

   
   
   

   4. n₁ = 8 and n₂ = 2

   
   
   

---

1. View Hint View Answer Discuss in Forum

   ∴ T ∝ n³
   

   	T1	=	8T2	=		n1		3
   	T2		T2			n2

   
   Hence, n₁ = 2n₂
   

   Correct Option: A

   ∴ T ∝ n³
   

   	T1	=	8T2	=		n1		3
   	T2		T2			n2

   
   Hence, n₁ = 2n₂
   

---

2. ​An electron of a stationary hydrogen atom passes from the fifth energy level to the ground level. The velocity that the atom acquired as a result of photon emission will be :​
   (m is the mass of the electron, R, Rydberg constant and h Planck’s constant)

1. 1. 	24hR
      	25m

   
   
   

   2. 	25hR
      	24m

   
   
   

   3. 	25m
      	24hR

   
   
   

   4. 	24m
      	25hR

   
   
   

---

1. View Hint View Answer Discuss in Forum

   For emission, the wave number of the radiation is given as
   

   	1	= RZ2		1	-	1
   	λ			n21		n22

   
   R = Rydberg constant, Z = atomic number
   

   = R		1	-	1
   		12		52

   
   

   = R		1 -	1
   			25

   
   

   ⇒	1	= R	24
   	λ		25

   
   linear momentum
   

   P =	h	= h × R ×	24
   	λ		25

   
   (de-Broglie hypothesis)
   

   ⇒ mv =	24hR	⇒ V =	24hR
   	25		25m

   Correct Option: A

   For emission, the wave number of the radiation is given as
   

   	1	= RZ2		1	-	1
   	λ			n21		n22

   
   R = Rydberg constant, Z = atomic number
   

   = R		1	-	1
   		12		52

   
   

   = R		1 -	1
   			25

   
   

   ⇒	1	= R	24
   	λ		25

   
   linear momentum
   

   P =	h	= h × R ×	24
   	λ		25

   
   (de-Broglie hypothesis)
   

   ⇒ mv =	24hR	⇒ V =	24hR
   	25		25m

---

---

3. Electron in hydrogen atom first jumps from third excited state to second excited state and then from second excited to the first excited state. The ratio of the wavelength  λ₁ : λ₂ emitted in the two cases is

1. 1. 7/5

   
   
   

   2. 27/20 ​

   
   
   

   3. 27/5 ​

   
   
   

   4. 20/7

   
   
   

---

1. View Hint View Answer Discuss in Forum

   
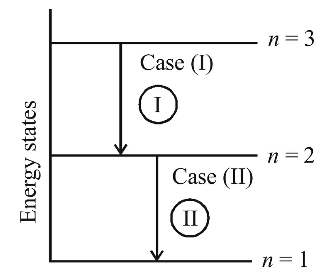
   The wave number (V) of the radiation
   

   =	1
   	λ

   
   
   

   ⇒	λ1	=	36	×	3R∞
   	λ2		5R∞		4

   
   

   	λ1	=	27
   	λ2		5

   Correct Option: C

   
   The wave number (V) of the radiation
   

   =	1
   	λ

   
   
   

   ⇒	λ1	=	36	×	3R∞
   	λ2		5R∞		4

   
   

   	λ1	=	27
   	λ2		5

---

4. ​The transition from the state n = 3 to n = 1 in a hydrogen like atom results in ultraviolet radiation. Infrared radiation will be obtained in the transition from :​​

1. 1. 2 → 1

   
   
   

   2. 3 → 2 ​

   
   
   

   3. 4 → 2 ​

   
   
   

   4. 4 → 3

   
   
   

---

1. View Hint View Answer Discuss in Forum

   ∵ The frequency of the transition
   

   V ∝	1
   	n2

   
   when n = 1, 2, 3.

   Correct Option: D

   ∵ The frequency of the transition
   

   V ∝	1
   	n2

   
   when n = 1, 2, 3.

---

---

5. Hydrogen atom in ground state is excited by a monochromatic radiation of λ = 975 Å. Number of spectral lines in the resulting spectrum emitted will be

1. 1. 3

   
   
   

   2. 2

   
   
   

   3. 6

   
   
   

   4. 10

   
   
   

---

1. View Hint View Answer Discuss in Forum

   For the λ = 975 Å
   

   	1	= R		1	-	1
   	λ			n21		n22

   
   where R is the Rydberg constant ​
   Solving we get n₂ = n = 4 ​
   (∵ n₁ = 1 ground state) ​
   Therefore number of spectral lines
   

   =	n(n - 1)	=	4(4 - 1)	= 6
   	2		2

   Correct Option: C

   For the λ = 975 Å
   

   	1	= R		1	-	1
   	λ			n21		n22

   
   where R is the Rydberg constant ​
   Solving we get n₂ = n = 4 ​
   (∵ n₁ = 1 ground state) ​
   Therefore number of spectral lines
   

   =	n(n - 1)	=	4(4 - 1)	= 6
   	2		2

---