Atoms
- The transition from the state n = 3 to n = 1 in a hydrogen like atom results in ultraviolet radiation. Infrared radiation will be obtained in the transition from :
-
View Hint View Answer Discuss in Forum
∵ The frequency of the transition
V ∝ 1 n2
when n = 1, 2, 3.Correct Option: D
∵ The frequency of the transition
V ∝ 1 n2
when n = 1, 2, 3.
- The wavelength of the first line of Lyman series for hydrogen atom is equal to that of the second line of Balmer series for a hydrogen like ion. The atomic number Z of hydrogen like ion is
-
View Hint View Answer Discuss in Forum
For first line of Lyman series of hydrogen
hc = Rhc 
1 - 1 
λ1 12 22
For second line of Balmer series of hydrogen like ionhc = R2hc 
1 - 1 
λ2 22 42
By question, λ1 = λ2⇒ 
1 - 1 
1 2 = Z2 
1 - 1 
or Z = 2 4 16 Correct Option: D
For first line of Lyman series of hydrogen
hc = Rhc 
1 - 1 
λ1 12 22
For second line of Balmer series of hydrogen like ionhc = R2hc 
1 - 1 
λ2 22 42
By question, λ1 = λ2⇒ 
1 - 1 
1 2 = Z2 
1 - 1 
or Z = 2 4 16
- An electron in the hydrogen atom jumps from excited state n to the ground state. The wavelength so emitted illuminates a photosensitive material having work function 2.75 eV. If the stopping potential of the photoelectron is 10 V, the value of n is
-
View Hint View Answer Discuss in Forum
KEmax = 10eV
φ = 2.75 eV
Total incident energy
E = φ + KEmax = 12.75 eV
∴ Energy is released when electron jumps from the excited state n to the ground state.
E4 – E4 = {– 0.85 – (–13.6) ev} = 12.75 eV
∴ value of n = 4Correct Option: B
KEmax = 10eV
φ = 2.75 eV
Total incident energy
E = φ + KEmax = 12.75 eV
∴ Energy is released when electron jumps from the excited state n to the ground state.
E4 – E4 = {– 0.85 – (–13.6) ev} = 12.75 eV
∴ value of n = 4
- Out of the following which one is not a possible energy for a photon to be emitted by hydrogen atom according to Bohr’s atomic model?
-
View Hint View Answer Discuss in Forum
Obviously, difference of 11.1eV is not possible.
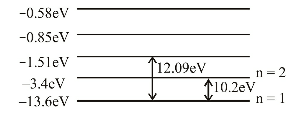
Correct Option: B
Obviously, difference of 11.1eV is not possible.

- The energy of a hydrogen atom in the ground state is – 13.6 eV. The energy of a He+ ion in the first excited state will be
-
View Hint View Answer Discuss in Forum
Energy of a H-like atom in it's nth state is given by
En = -Z2 × 13.6 eV n2
For, first excited state of He+, n = 2, Z = 2EHe+ = - 4 × 13.6 = - 13.6 eV 22 Correct Option: A
Energy of a H-like atom in it's nth state is given by
En = -Z2 × 13.6 eV n2
For, first excited state of He+, n = 2, Z = 2EHe+ = - 4 × 13.6 = - 13.6 eV 22

