Engineering Mathematics Miscellaneous
- If z is a complex variable, the value of
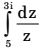
-
View Hint View Answer Discuss in Forum
3i∫5 dz = In(z) 
3i = In 3i - In 5 z 5 = In 3 + i π - (ln 5 + i0) 2
[∴ In z = In r iθ where r = √x² + y², 0 argz]= In 3 - In 5 + i 22 = - 0.511 + 157i 14 Correct Option: B
3i∫5 dz = In(z) 
3i = In 3i - In 5 z 5 = In 3 + i π - (ln 5 + i0) 2
[∴ In z = In r iθ where r = √x² + y², 0 argz]= In 3 - In 5 + i 22 = - 0.511 + 157i 14
-
Finding the solution of d²y + 16y = 0 for y(x) with the two boundary dx² conditions dy |x=0 = 1 and dy |x=π/2 = - 1 has dx dx
-
View Hint View Answer Discuss in Forum
(D² + 16)y = 0
A.E. → D² + 16 = 0
⇒ D = ± 4i
y = C1cos 4x + C2 sin 4xdy = -4C1sin 4x + 4C2 cos 4x dx dy |x=0 = -4C1 × 0 + 4C2 × 1 = 4C2 dx
4C2 = 1
C2 = 1/4
Now,dy |x=π/2 = -4C1 × sin4/2 + 4C2 × cos = 4/2 dx dy |x=π/2 = 0 + 4C2 = 4(1/2) = 1 dx But dy |x=π/2 = - 1 (Given) dx
Hence no solution.Correct Option: A
(D² + 16)y = 0
A.E. → D² + 16 = 0
⇒ D = ± 4i
y = C1cos 4x + C2 sin 4xdy = -4C1sin 4x + 4C2 cos 4x dx dy |x=0 = -4C1 × 0 + 4C2 × 1 = 4C2 dx
4C2 = 1
C2 = 1/4
Now,dy |x=π/2 = -4C1 × sin4/2 + 4C2 × cos = 4/2 dx dy |x=π/2 = 0 + 4C2 = 4(1/2) = 1 dx But dy |x=π/2 = - 1 (Given) dx
Hence no solution.
- If y = f(x) satisfies the boundary value problem
y" + 9y = 0, y(0), y 
π 
= √2 then they 
π 
is 2 4
-
View Hint View Answer Discuss in Forum
y" + 9y = 0
A.E. is m² + 9 = 0
m = ±3i
y = yc + yp
y = C1 cos3x + C2 sin3x
(∵ yp = 0)
If x = 0, y = 0
0 C1(1) + C2(0) ⇒ C1 = 0
If x = π/2, y = √2
√2 = C1(0) + C2sin(3π/2) ⇒ C2 = - √2
∴ y = - √2 sin3x
If x = (π/4) = - √2 (3π/4) = √2(1/√2) = - 1Correct Option: A
y" + 9y = 0
A.E. is m² + 9 = 0
m = ±3i
y = yc + yp
y = C1 cos3x + C2 sin3x
(∵ yp = 0)
If x = 0, y = 0
0 C1(1) + C2(0) ⇒ C1 = 0
If x = π/2, y = √2
√2 = C1(0) + C2sin(3π/2) ⇒ C2 = - √2
∴ y = - √2 sin3x
If x = (π/4) = - √2 (3π/4) = √2(1/√2) = - 1
-
u = U 
1 + ekx 
1 - ekL
which passes through the origin and the point
In 2, 3 
4
-
View Hint View Answer Discuss in Forum
d²y = y ⇒ (D² - 1)y = 0 dx²
D² – 1 = 0
⇒ D = ± 1
y = c1 ex + c2 e–xPasses through (0, 0) and 
142, 3 
(0,0) 4
⇒ 0 = C1 + C2 ...(1)
142, 3 
(0,0) 4 3 = C1 + C2e-142 = C1 2 + C2 4 2 ⇒ 2C1 + 1 C2 = 3 2 4
solving (1) and (2)
⇒ C1 = 1/2
C2 = – 1/2∴ y = 1 ex - 1 e-x = 1 (ex - e-x) 2 2 2 Correct Option: C
d²y = y ⇒ (D² - 1)y = 0 dx²
D² – 1 = 0
⇒ D = ± 1
y = c1 ex + c2 e–xPasses through (0, 0) and 
142, 3 
(0,0) 4
⇒ 0 = C1 + C2 ...(1)
142, 3 
(0,0) 4 3 = C1 + C2e-142 = C1 2 + C2 4 2 ⇒ 2C1 + 1 C2 = 3 2 4
solving (1) and (2)
⇒ C1 = 1/2
C2 = – 1/2∴ y = 1 ex - 1 e-x = 1 (ex - e-x) 2 2 2

