Engineering Mathematics Miscellaneous
- Using the trapezoidal rule, and dividing the interval of integration into three equal subintervals, the definite integral
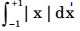is_____ .
-
View Hint View Answer Discuss in Forum
∫+1-1|x|dx
Let y = |x|
n = no. of subintervals = 3h = xn - n0 = 1 - (-1) = 2 n 3 3
Values of x are,-1, -1 + 2 , 1 + 2 
2 
, - 1 + 3 2 3 3 3 
= ∫xnx0 f(x) dx = h/2[y0 + yn + 2 (y1 + ..... + yn-1)]
|x| dx = 1 
(1 + 1) + 2 1 + 1 
3 3 3 = 1 2 + 4 = 1 × 10 = 10 = 1.1111 3 3 3 3 9 Correct Option: B
∫+1-1|x|dx
Let y = |x|
n = no. of subintervals = 3h = xn - n0 = 1 - (-1) = 2 n 3 3
Values of x are,-1, -1 + 2 , 1 + 2 2 , - 1 + 3 2 3 3 3
= ∫xnx0 f(x) dx = h/2[y0 + yn + 2 (y1 + ..... + yn-1)]|x| dx = 1 (1 + 1) + 2 1 + 1 3 3 3 = 1 2 + 4 = 1 × 10 = 10 = 1.1111 3 3 3 3 9
- The definite integral
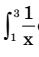is evaluated using trapezoidal rule with a step size of 1. The correct answer is ________.
-
View Hint View Answer Discuss in Forum
Given : ∫³1 1 dx x
h = step size 1
n = no. of sub intervals= 3 - 1 = 2 1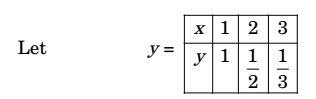 
By trapezoidal rule
∫xnx0 f(x) dx = h/2[(y0 + yn) + 2(y1 + ...........+ yn-1)]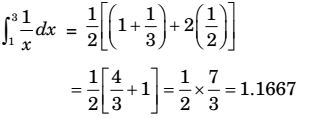
Correct Option: D
Given : ∫³1 1 dx x
h = step size 1
n = no. of sub intervals= 3 - 1 = 2 1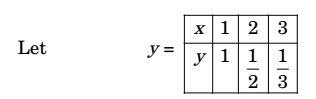
By trapezoidal rule
∫xnx0 f(x) dx = h/2[(y0 + yn) + 2(y1 + ...........+ yn-1)]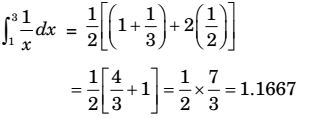
- The integral
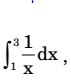when evaluated by using Simpson's 1/3 rule on two equal subintervals each of length 1, equals
-
View Hint View Answer Discuss in Forum
Given : ∫³1 1 dx x
Here, a = 1, b = 3, n = 2h = b -a = 1 n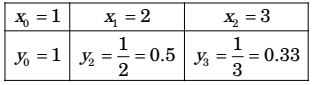 
By Simpson's rule∫³1 1 dx = 1 h[ y1 + y3) + 4(y2)] x 3 = 1 (1) [(1 + 0.33) + 4 (0.51)] = 1.11 3 Correct Option: C
Given : ∫³1 1 dx x
Here, a = 1, b = 3, n = 2h = b -a = 1 n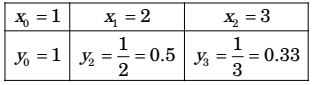
By Simpson's rule∫³1 1 dx = 1 h[ y1 + y3) + 4(y2)] x 3 = 1 (1) [(1 + 0.33) + 4 (0.51)] = 1.11 3
- Torque exerted on a flywheel over a cycle is listed in the table. Flywheel energy (in J per unit cycle) using Simpson's rule is Angle (degree)
-
View Hint View Answer Discuss in Forum
Given: h = 60° – 0° = 60° = 60 × π/180 = 1.047
y0 = 0, y1 = 1066, y2 = – 323, y4 = 323, y5 = – 355, y6 = 0
By Simpson’s rule, flywheel energy
= h/3[(y0 + y6) + 4(y1 + y3 + y5) + 2(y2 + y4)]
= 1.047/3 [(0 + 0) + 4(1066 + 0 - 355) + 2(- 323 + 323)
= 993 Nm rad
= 993 Joules/cycleCorrect Option: B
Given: h = 60° – 0° = 60° = 60 × π/180 = 1.047
y0 = 0, y1 = 1066, y2 = – 323, y4 = 323, y5 = – 355, y6 = 0
By Simpson’s rule, flywheel energy
= h/3[(y0 + y6) + 4(y1 + y3 + y5) + 2(y2 + y4)]
= 1.047/3 [(0 + 0) + 4(1066 + 0 - 355) + 2(- 323 + 323)
= 993 Nm rad
= 993 Joules/cycle
- The number of accidents occurring in a plant in a month follows Poisson distribution with mean as 5.2. The probability of occurrence of less than 2 accidents in the plant during a randomly selected month is
-
View Hint View Answer Discuss in Forum
Given λ = 5.2
Let x be random variable which follows Poisson’s distribution
P(x < 2) = P(x = 0) + P(x = 1)= e-λλ0 + e-λ = e-5.2 (6.2) 0! 1!
= 0.0055 × 6.2 = 0.034Correct Option: B
Given λ = 5.2
Let x be random variable which follows Poisson’s distribution
P(x < 2) = P(x = 0) + P(x = 1)= e-λλ0 + e-λ = e-5.2 (6.2) 0! 1!
= 0.0055 × 6.2 = 0.034
