26. Let X be a normal random variable with mean 1 and variance 4. The probability P{X < 0} is

1. 1. 0.5

   
   
   

   2. greater then a zero and less than 0.5

   
   
   

   3. greater than 0.5 and less than 1.0

   
   
   

   4. 1.0

   
   
   

---

1. View Hint View Answer Discuss in Forum

   P (x <0) = P		(X - X)	<	0 - X
   		σ		σ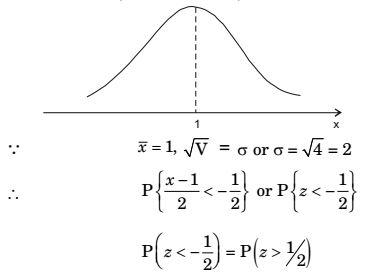

   
   
   ∵ P (x > a) represents area under curve for x > a

   Correct Option: B

   P (x <0) = P		(X - X)	<	0 - X
   		σ		σ

   
   
   ∵ P (x > a) represents area under curve for x > a

---

27. The Laplace transform of tet is

1. 1. s

      (s + 1)²

   
   
   

   2. 1

      (s - 1)²

   
   
   

   3. 1

      (s + 1)²

   
   
   

   4. s

      s - 1

   
   
   

---

1. View Hint View Answer Discuss in Forum

   Laplace transform of t = 1/S²
   By applying shift property
   we get
   

   L[tet] =	1
   	(s - 1)²

   Correct Option: B

   Laplace transform of t = 1/S²
   By applying shift property
   we get
   

   L[tet] =	1
   	(s - 1)²

---

---

28. A six-faced fair dice is rolled five times. The probability (in%) of obtaining "ONE" at least four times is

1. 1. 33.3

   
   
   

   2. 3.33

   
   
   

   3. 0.33

   
   
   

   4. 0.0033

   
   
   

---

1. View Hint View Answer Discuss in Forum

   A dice is rolled 5 times
   n = 5
   P = (Probability of getting 1) = 1/6
   

   0% q = 1 - p = 1 -	1	=	5
   	6		6

   
   Probability of getting 1 at least 4 times is
   P(x ≥ 4) = P(x = 4) + P(x = 5)
   = ⁿC₄p⁴q^n-4 + ⁿC₅p⁵q^n-5[∵ ⁿC_rp_xq_n-x
   = ⁵C₄p⁴q⁰
   

   = 5 ×		1		4			5		1	+ 1 ×		1		5			5		0
   		6					6					6					6

   
   

   =	25	+	1	=	26	= 0.0033
   	(6)5		(6)5		(6)5

   
   Required probability = 0.33%

   Correct Option: C

   A dice is rolled 5 times
   n = 5
   P = (Probability of getting 1) = 1/6
   

   0% q = 1 - p = 1 -	1	=	5
   	6		6

   
   Probability of getting 1 at least 4 times is
   P(x ≥ 4) = P(x = 4) + P(x = 5)
   = ⁿC₄p⁴q^n-4 + ⁿC₅p⁵q^n-5[∵ ⁿC_rp_xq_n-x
   = ⁵C₄p⁴q⁰
   

   = 5 ×		1		4			5		1	+ 1 ×		1		5			5		0
   		6					6					6					6

   
   

   =	25	+	1	=	26	= 0.0033
   	(6)5		(6)5		(6)5

   
   Required probability = 0.33%

---

29. Two coins are tossed simultaneously. The probability (upto two decimal points accuracy) of getting at least one head is ___.

1. 1. 1.25

   
   
   

   2. 1.75

   
   
   

   3. 0.75

   
   
   

   4. 1

   
   
   

---

1. View Hint View Answer Discuss in Forum

   Considering all Sample Space, we gets
   {HH, HT, TH, TT}
   For at least one head, probability is 3/4
   P (at least one head) = 0.75

   Correct Option: C

   Considering all Sample Space, we gets
   {HH, HT, TH, TT}
   For at least one head, probability is 3/4
   P (at least one head) = 0.75

---

---

30. A six-face fair dice is rolled a large number of times. The mean value of the outcomes is ___.

1. 1. 3.9

   
   
   

   2. 3.6

   
   
   

   3. 3.5

   
   
   

   4. 3.4

   
   
   

---

1. View Hint View Answer Discuss in Forum

   
   We know that
   μ = ∑x.p(x)
   = (1 + 2 + 3 + 4 + 5 + 6) × 1/6 = 1
   21 × 1/6 = 3.5

   Correct Option: C

   
   We know that
   μ = ∑x.p(x)
   = (1 + 2 + 3 + 4 + 5 + 6) × 1/6 = 1
   21 × 1/6 = 3.5

---