Engineering Mathematics Miscellaneous
-
Eigenvalues of a matrix S = 
3 2 
are 5 and 1. 2 3
What are the eigenvalues of the matrix S² = SS?
-
View Hint View Answer Discuss in Forum
For S matrix, if eigen values are λ1, λ2, λ3,... then for S² matrix, the eigen values will be λ²1 λ²2 λ²3 ,, ,....
For S matrix, if eigen values are 1 and 5 then for S² matrix, the eigen values are 1 and 25Correct Option: A
For S matrix, if eigen values are λ1, λ2, λ3,... then for S² matrix, the eigen values will be λ²1 λ²2 λ²3 ,, ,....
For S matrix, if eigen values are 1 and 5 then for S² matrix, the eigen values are 1 and 25
- The set of equations
x + y + z = 1
a – ay + 3z = 5
5x – 3y + az = 6
has infinite solution, if a =
-
View Hint View Answer Discuss in Forum
Given set of equations are,
x + y + z = 1, a – ay + 32 = 5 and 5x – 3y + az = 6
Now ρ(A) = ρ(AB) < no. of variables
| A| = 0
1 1 1 
= 0 a -a 3 5 -3 a
(– a² + 9) – (a² – 15) + (– 3a + 5a) = 0
9 – a² + 15 – a² + 2a = 0
2a² – 2a – 24 = 0
a² – a – 12 = 0
a² – 4a + 3a – 12 = 0
(a = 4, – 3)
ρ(AB) < (No. of variable)1 1 1 = 0 -a 3 5 -3 a 6
1(18 – 5a) – 1(– 6a + 15) + 1(– a² + 9) = 0
18 – 5a – 15 + 6a + 9 – a² = 0
a² – a – 12 = 0
a = 3, 4 or a = 41 1 1 = 0 a -a 5 5 -3 6
(– 6a + 15) – (6a – 25) + (– 3a + 5a) = 0
– 6a + 15 – 6a + 25 + 2a = 0
10a = 40
a = 4
if a = 4
| AB| = 01 1 1 = 0 a 3 5 5 a 6
(18 – 5a) – (6a – 25) + (a² – 15) = 0
a² – 11a + 28 = 0
a = 7, 4 or a = 4Correct Option: C
Given set of equations are,
x + y + z = 1, a – ay + 32 = 5 and 5x – 3y + az = 6
Now ρ(A) = ρ(AB) < no. of variables
| A| = 01 1 1 = 0 a -a 3 5 -3 a
(– a² + 9) – (a² – 15) + (– 3a + 5a) = 0
9 – a² + 15 – a² + 2a = 0
2a² – 2a – 24 = 0
a² – a – 12 = 0
a² – 4a + 3a – 12 = 0
(a = 4, – 3)
ρ(AB) < (No. of variable)1 1 1 = 0 -a 3 5 -3 a 6
1(18 – 5a) – 1(– 6a + 15) + 1(– a² + 9) = 0
18 – 5a – 15 + 6a + 9 – a² = 0
a² – a – 12 = 0
a = 3, 4 or a = 41 1 1 = 0 a -a 5 5 -3 6
(– 6a + 15) – (6a – 25) + (– 3a + 5a) = 0
– 6a + 15 – 6a + 25 + 2a = 0
10a = 40
a = 4
if a = 4
| AB| = 01 1 1 = 0 a 3 5 5 a 6
(18 – 5a) – (6a – 25) + (a² – 15) = 0
a² – 11a + 28 = 0
a = 7, 4 or a = 4
- Four red balls, four green balls and four blue balls are put in a box. Three balls are pulled out of the box at random one after another without replacement. The probability that all the three balls are red is
-
View Hint View Answer Discuss in Forum
(4R, 4G, 4B)
P(RRR) (without replacement)= 4C1 × 3C1 × 2C1 = 1 12C1 11C1 10C1 55 Correct Option: B
(4R, 4G, 4B)
P(RRR) (without replacement)= 4C1 × 3C1 × 2C1 = 1 12C1 11C1 10C1 55
- Solutions of Laplace's equation having continuous second-order partial derivatives are called
-
View Hint View Answer Discuss in Forum
The solution of Laplace’s equation having continuous 2nd order partial derivatives is called a harmonic function.
Correct Option: B
The solution of Laplace’s equation having continuous 2nd order partial derivatives is called a harmonic function.
- The value of
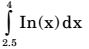calculated using the Trapezoidal rule with five subintervals is ___.
-
View Hint View Answer Discuss in Forum
Given
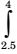In x dx n = 5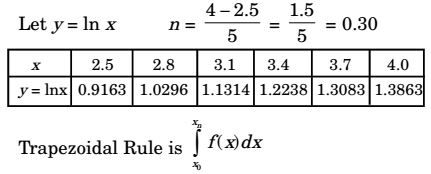
= h [(y0 + yn) + 2y1 + ...... + yn-1] 2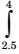 
In x dx= 0.3 (0.9163 + 1.3863) (1.0296 + 1.314 + 1.2238 + 1.3083) 2
= 0.15 (2.3026 + 9.3862) = 1.7533Correct Option: B
Given
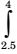In x dx n = 5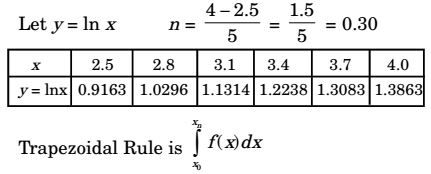= h [(y0 + yn) + 2y1 + ...... + yn-1] 2 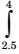In x dx= 0.3 (0.9163 + 1.3863) (1.0296 + 1.314 + 1.2238 + 1.3083) 2
= 0.15 (2.3026 + 9.3862) = 1.7533
