Engineering Mathematics Miscellaneous Difficult Questions and Answers | Page - 2

Engineering Mathematics Miscellaneous

The vector field F = xî - yĵ (where î and ĵ are unit vector) is

1. divergence free, but not irrotational
1. irrotational, but not divergence free
1. divergence free and irrotational
1. neither divergence free nor irrotational

View Hint View Answer Discuss in Forum

F = xi - yj
For divergence:-
grade F = ∇F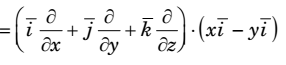

Hence vector field is divergence free
For is rotational,
Curl F = ∇ × F

Hence vector field is irrotational.

Correct Option: C

F = xi - yj
For divergence:-
grade F = ∇F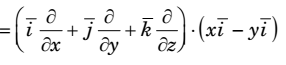

Hence vector field is divergence free
For is rotational,
Curl F = ∇ × F

Hence vector field is irrotational.

The directional derivative of the function f(x, y) = x² + y² along a line directed from (0, 0) to (1, 1), evaluated at the point x = 1, y = 1 is

1. 2
1. 4√2
1. 2√2
1. √2

View Hint View Answer Discuss in Forum

Directional derivative = ∇f. a
|a|

∇f = δx² ̂i + δy² ̂j
δx δy

= 2xî + 2yĵ
a = line joining (0,0) and (1,1)
1î + 1ĵ
a = î + ĵ
Directional derivative = (2xî + 2yĵ)(î + ĵ)
√2

= 2x + 2y
√2

Directional derivative at (1,1) = 2 + 2 = 2√2
√2

Correct Option: C

Directional derivative = ∇f. a
|a|

∇f = δx² ̂i + δy² ̂j
δx δy

= 2xî + 2yĵ
a = line joining (0,0) and (1,1)
1î + 1ĵ
a = î + ĵ
Directional derivative = (2xî + 2yĵ)(î + ĵ)
√2

= 2x + 2y
√2

Directional derivative at (1,1) = 2 + 2 = 2√2
√2

The value of ∫[(3x - 8y²)dx (4y - 6xy) dy] (where C is the boundary of the region boundary by x = 0, y = 0 and x + y = 1) is ________.

1. 1.524
1. 3.66
1. 1.666
1. 2.65

View Hint View Answer Discuss in Forum

∫_c[(3x - 8y²)dx + (4y - 6xy)dy],
C is boundary of region bounded by x = 0, y =1, and z + y = 1
By using Green's theoren, we get
I = ∮_c(pdx + Qdy) dx = ∮_R∮ δQ -δP dx dy
δv δy

Her P = 3x – 8y²
Q = 4y – 6xy
δQ = -6y
δx

δP = -16y
δx

I = ∫∫(-6y -(16y)dx dy
I = ∫∫ 10y dx dy
I = 10¹∫₀dx^1-x∫₀ y²
2

I = 5¹∫₀dx(1 - x)²
I = 1.666

Correct Option: B

∫_c[(3x - 8y²)dx + (4y - 6xy)dy],
C is boundary of region bounded by x = 0, y =1, and z + y = 1
By using Green's theoren, we get
I = ∮_c(pdx + Qdy) dx = ∮_R∮ δQ -δP dx dy
δv δy

Her P = 3x – 8y²
Q = 4y – 6xy
δQ = -6y
δx

δP = -16y
δx

I = ∫∫(-6y -(16y)dx dy
I = ∫∫ 10y dx dy
I = 10¹∫₀dx^1-x∫₀ y²
2

I = 5¹∫₀dx(1 - x)²
I = 1.666

Consider an ant crawling along the curve (x – 2)² + y² = 4, where x and y are in meters. The ant starts at the point (4, 0) and moves counter– clockwise with a speed of 1.57 meters per second. The time taken by the ant to reach the point (2, 2) is (in seconds) ________.

1. 3 sec
1. 3.5 sec
1. 2 sec
1. 2.5sec

View Hint View Answer Discuss in Forum

1 × circumference
4

⇒ 1 × π × 4
4

time = π = 2sec
1.5 →

1 × circumference
4

⇒ 1 × π × 4
4

time = π = 2sec
1.5 →

Correct Option: C

1 × circumference
4

⇒ 1 × π × 4
4

time = π = 2sec
1.5 →

Eigenvalues of a matrix S = 3 2 are 5 and 1.
2 3

What are the eigenvalues of the matrix S² = SS?

1. 1 and 25
1. 6 and 4
1. 5 and 1
1. 2 and 10

View Hint View Answer Discuss in Forum

For S matrix, if eigen values are λ₁, λ₂, λ₃,... then for S² matrix, the eigen values will be λ²₁ λ²₂ λ²₃ ,, ,....
For S matrix, if eigen values are 1 and 5 then for S² matrix, the eigen values are 1 and 25

Correct Option: A

For S matrix, if eigen values are λ₁, λ₂, λ₃,... then for S² matrix, the eigen values will be λ²₁ λ²₂ λ²₃ ,, ,....
For S matrix, if eigen values are 1 and 5 then for S² matrix, the eigen values are 1 and 25