Engineering Mathematics Miscellaneous
- F(s) is the Laplace transform of the function f(t) = 2t²e–t
F(1) is _______(correct to two decimal places.)
-
View Hint View Answer Discuss in Forum
Applying Laplace transform
L[ten] = n! Sn+1 L[t²] = 2 S³ L[2t²] = 4 S³ F(S) = L[e-t.2t²] = 4 (S + 1)³
Putting s = 1 we getF(1) = 4 = 4 = 0.5 (1 + 1)³ 8 Correct Option: B
Applying Laplace transform
L[ten] = n! Sn+1 L[t²] = 2 S³ L[2t²] = 4 S³ F(S) = L[e-t.2t²] = 4 (S + 1)³
Putting s = 1 we getF(1) = 4 = 4 = 0.5 (1 + 1)³ 8
- A parabola x = y² with 0 ≤ x ≤ 1 is shown in the figure. The volume of the solid of rotation obtained by rotating the shaded area by 360° around the x-axis is
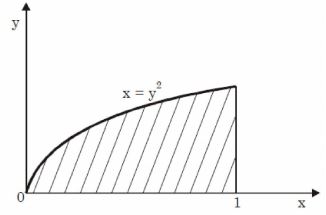
-
View Hint View Answer Discuss in Forum
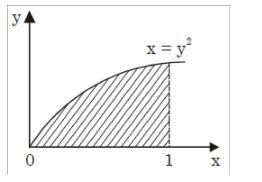
Here, volume of solid of rotation by rotating shaded area by 360° around x-axis is,
V = 1∫0πy²dxV = 1∫0 πx dx = πx² 
² = π 2 0 2 Correct Option: B

Here, volume of solid of rotation by rotating shaded area by 360° around x-axis is,
V = 1∫0πy²dxV = 1∫0 πx dx = πx² 
² = π 2 0 2
- The value of the following definite integral is _____ (round off to there decimal places).
e∫1(xInx)dx
-
View Hint View Answer Discuss in Forum
I = e∫1x In xdx
= In x² - ∫ 
1 × x² 
dx 2 x 2 = x² In x - x² 
e 2 1 4 = 
e² - e² 
+ 1 2 4 4 = e² + 1 = 2.097 4 Correct Option: C
I = e∫1x In xdx
= In x² - ∫ 
1 × x² 
dx 2 x 2 = x² In x - x² 
e 2 1 4 = 
e² - e² 
+ 1 2 4 4 = e² + 1 = 2.097 4
-
and nˆ as the unit normal vector to the surface of the hemisphere (x² + y² + z² = 1; z ≥ 0), the value of integral ∫(∇ × u) nˆ dS evaluated on the curved surface of the hemisphere S isGiven a vector U = 1 (-y³î + x³ĵ + z³̂k) 3
-
View Hint View Answer Discuss in Forum
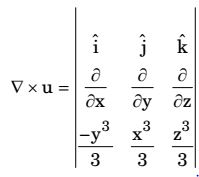
= 0 + 0 + (x² + y²)k̂
n̂ = k̂
∇ × u). n̂ = (∇ × v). k̂ = x² + y²
∫∫(x² + y²)dx dy
2π∫01∫0r²(rdrdθ) = π/2Correct Option: C
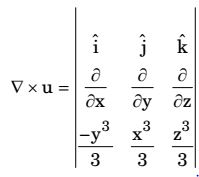
= 0 + 0 + (x² + y²)k̂
n̂ = k̂
∇ × u). n̂ = (∇ × v). k̂ = x² + y²
∫∫(x² + y²)dx dy
2π∫01∫0r²(rdrdθ) = π/2
- It is given that y + 2 y' = 0, y = 0, y(0) = 0, y(1)= 0. What is y(0.5)?
-
View Hint View Answer Discuss in Forum
y" + 2y' + y = 0
A.E is, D² + 2D + 1 = 0
⇒ (D + 1)² = 0
⇒ m = – 1
The C.F. is (C1 + C2 x)e–x and P.I. = 0
Now y(0) = 0
⇒ C1 = 0 a
nd y(1) = 0
⇒ C2 e–1 = 0,
⇒ C2 = 0
⇒ C.F. = 0
⇒ y(0.5) = 0Correct Option: A
y" + 2y' + y = 0
A.E is, D² + 2D + 1 = 0
⇒ (D + 1)² = 0
⇒ m = – 1
The C.F. is (C1 + C2 x)e–x and P.I. = 0
Now y(0) = 0
⇒ C1 = 0 a
nd y(1) = 0
⇒ C2 e–1 = 0,
⇒ C2 = 0
⇒ C.F. = 0
⇒ y(0.5) = 0

