Engineering Mathematics Miscellaneous Moderate Questions and Answers | Page - 5

Engineering Mathematics Miscellaneous

A function f of the complex variable z = x + iy, is given as f(x, y) = u(x, y) + iv(x, y), where u(x, y) = 2 kxy and v(x, y) = x² – y². The value of k, for which the function is analytic, is_____

1. - 1
1. - 2
1. - 3
1. - 4

View Hint View Answer Discuss in Forum

Given that f (z) = u + i v is analytic
u (x,y) = 2 kxy       v = x² – y²
u_x = 2ky       v_y = – 2y
ux = v_y
k = –1
u_y = 2kx       v_x = 2x
u_y = –vx
2kx = –2x
k = –1

Correct Option: A

Given that f (z) = u + i v is analytic
u (x,y) = 2 kxy       v = x² – y²
u_x = 2ky       v_y = – 2y
ux = v_y
k = –1
u_y = 2kx       v_x = 2x
u_y = –vx
2kx = –2x
k = –1

A harmonic function is analytic if it satisfies the Laplace equation. If u(x, y) = 2x² – 2y² + 4xy is a harmonic function, t hen its conjugate harmonic function v (x, y) is

1. 4y² – 4xy + constant
1. 4xy – 2x² + 2y² + constant
1. 2x² – 2y² + xy + constant
1. – 4xy + 2y² – 2x² + constant

View Hint View Answer Discuss in Forum

u(x, y) = 2x² – 2y² + 4xy
As harmonic function is analytic therefore,
u_x = V_y
u_y = – V_x
u_x = 4x + 4y
δv V_y = 4x + 4y
δy

V = 4xy + 2y² + f(x)
Now
δv V_y + f'(x) = 4y - 4x
δy

f'(x) = – 4x
f(x) = – 2x²2 + C
So, conjugate harmonic function v(x, y) is,
V = 2y² – 2x² + 4xy + C

Correct Option: B

u(x, y) = 2x² – 2y² + 4xy
As harmonic function is analytic therefore,
u_x = V_y
u_y = – V_x
u_x = 4x + 4y
δv V_y = 4x + 4y
δy

V = 4xy + 2y² + f(x)
Now
δv V_y + f'(x) = 4y - 4x
δy

f'(x) = – 4x
f(x) = – 2x²2 + C
So, conjugate harmonic function v(x, y) is,
V = 2y² – 2x² + 4xy + C

An analytic function f(z) of complex variable z = x + iy may be written as f(z) = u(x, y) + iv(x, y). Then u(x, y) and v(x, y) must satisfy

1. δu = - δv and δu = δv
  δx δy δy δx
1. δu = δv and δu = - δv
  δx δy δy δx
1. δu = - δv and δu = - δv
  δx δy δy δx
1. δu = δv and δu = δv
  δx δy δy δx

View Hint View Answer Discuss in Forum

f(z) = u(x, y) + iv(x, y)
δu = δv ......(1)
δx δy

δu = - δv ......(1)
δy δx

Correct Option: B

f(z) = u(x, y) + iv(x, y)
δu = δv ......(1)
δx δy

δu = - δv ......(1)
δy δx

The integral ∮ f (z) dz evaluated around the unit circle on the complex plane for f(z) = cosz/z is

1. 2πi
1. 4πi
1. –2πi
1. 0

View Hint View Answer Discuss in Forum

f(z) = cosz has simple pole at z = 0
z

∴ Residue of f (z) at z = 0
Ltf (z) = Lt cos z = 1
z → 0 z → 0
= 2 π i (Residue at z = 0)

Correct Option: A

f(z) = cosz has simple pole at z = 0
z

∴ Residue of f (z) at z = 0
Ltf (z) = Lt cos z = 1
z → 0 z → 0
= 2 π i (Residue at z = 0)

The probability that a part manufactured by a company will be defective is 0.05. If such parts are selected randomly and inspected, then the probabilit y that at least t wo par ts will be defective is ____ (round off to two decimal places).

1. ≈ 2.17
1. ≈ 0.17
1. ≈ 1.25
1. ≈ 1.17

View Hint View Answer Discuss in Forum

(P)_defective = 0.05
(P)_{non-defective} = 1 – 0.05 = 0.95
Probability that atleast two parts will be defective,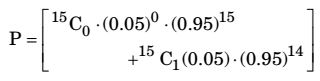

= 1 – 0.829
Required probability
P = 0.1709 ≈ 0.17

Correct Option: B

(P)_defective = 0.05
(P)_{non-defective} = 1 – 0.05 = 0.95
Probability that atleast two parts will be defective,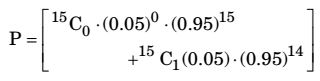

= 1 – 0.829
Required probability
P = 0.1709 ≈ 0.17