Engineering Mathematics Miscellaneous

Engineering Mathematics Miscellaneous

Easy Questions
Moderate Questions
Difficult Questions

Engineering Mathematics

Engineering Mathematics Miscellaneous
  1. Consider the continuous random variable with probability density function
    f(t) = 1 + t for – 1 ≤ t ≤ 0
    = 1 – t for 0 ≤ t ≤ 5 1
    The standard deviation of the random variable is








  1. View Hint View Answer Discuss in Forum

    Mean(t) ∞∫-1 t.f(t).dt = o∫-1(1 + t)dt 1∫ot(1 - t)dt

    Variance = ∞∫-∞(t - t)² f(t).dt
    o∫-1 t² (1 + t)dt + 1∫o t²(1 - t)dt = 1/6
    Stan dard deviation = √Variance =1/√6

    Correct Option: B

    Mean(t) ∞∫-1 t.f(t).dt = o∫-1(1 + t)dt 1∫ot(1 - t)dt

    Variance = ∞∫-∞(t - t)² f(t).dt
    o∫-1 t² (1 + t)dt + 1∫o t²(1 - t)dt = 1/6
    Stan dard deviation = √Variance =1/√6

  1. A nationalized bank has found that the daily balance available in its savings accounts follows a normal distribution with a mean of Rs. 500 and a standard deviation of Rs. 50. The percentage of savings account holders, who maintain an average daily balance more than Rs. 500 is ___.








  1. View Hint View Answer Discuss in Forum

    Given M = 500
    σ = 50
    P (X > 500) =?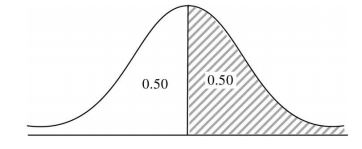

    Where X follows normal distribution
    We know that standard normal variable

    z =
    x - M
    σ

    z =
    500 - 500
    		 = 0
    50

    ∴ (X > 500) = P(z > 0) = 0.50 (see figure)

    Correct Option: D

    Given M = 500
    σ = 50
    P (X > 500) =?

    Where X follows normal distribution
    We know that standard normal variable

    z =
    x - M
    σ

    z =
    500 - 500
    		 = 0
    50

    ∴ (X > 500) = P(z > 0) = 0.50 (see figure)

  1. Match the correct pairs
    Numerical Integration SchemeOrder of Fitting Polynomial
    P. Simpson's 3/8 Rule1. First
    Q. Trapezoidal Rule2. Second
    R. Simpson's 1/3 Rule3. Third








  1. View Hint View Answer Discuss in Forum

    Trapezoidal rule fits linear polynomial (1st order) simplex 1/3 rule fits a parabolic curve (2nd order polynomial slip on 3/5 rule fit a able curve (3rd order polynomial
    ∴ Correct Answer ⇒ D

    Correct Option: D

    Trapezoidal rule fits linear polynomial (1st order) simplex 1/3 rule fits a parabolic curve (2nd order polynomial slip on 3/5 rule fit a able curve (3rd order polynomial
    ∴ Correct Answer ⇒ D

  1. Simpson's 1/3 rule is used to integrate the function f(x) = 3/5 x² + 9/5 between x = 0 and x = 1 using the least number of equal sub-intervals. The value of the integral is ______.








  1. View Hint View Answer Discuss in Forum

    Correct Option: C

  1. If f(t) is a function defined for all t > 0, its Laplace transform F(s) is defined as








  1. View Hint View Answer Discuss in Forum

    According to the Laplace transformation of
    f(t) ∀∈t≥0 is as F(s) = L{f(t)} =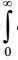 e-st f(t) dt

    Correct Option: B

    According to the Laplace transformation of
    f(t) ∀∈t≥0 is as F(s) = L{f(t)} =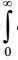 e-st f(t) dt