-
and nˆ as the unit normal vector to the surface of the hemisphere (x² + y² + z² = 1; z ≥ 0), the value of integral ∫(∇ × u) nˆ dS evaluated on the curved surface of the hemisphere S isGiven a vector U = 1 (-y³î + x³ĵ + z³̂k) 3
-
- - π/2
- π
- π/2
- π/3
Correct Option: C
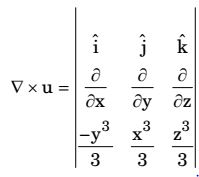
= 0 + 0 + (x² + y²)k̂
n̂ = k̂
∇ × u). n̂ = (∇ × v). k̂ = x² + y²
∫∫(x² + y²)dx dy
2π∫01∫0r²(rdrdθ) = π/2

