Numerical Ability
- There are 4 women P, Q, R, S and 5 men V, W, X, Y, Z in a group. We are required to form pairs each consisting of one woman and one man. P is not to be paired with Z, and Y must necessarily be paired with someone. In how many ways can 4 such pairs be formed?
-
View Hint View Answer Discuss in Forum
NA
Correct Option: C
NA
- In the graph below, the concentration of a particular pollutant in a lake is plotted over (alternate) days of a month in Winter (average temperature 10°C) and a month in summer (average temperature 30°C)
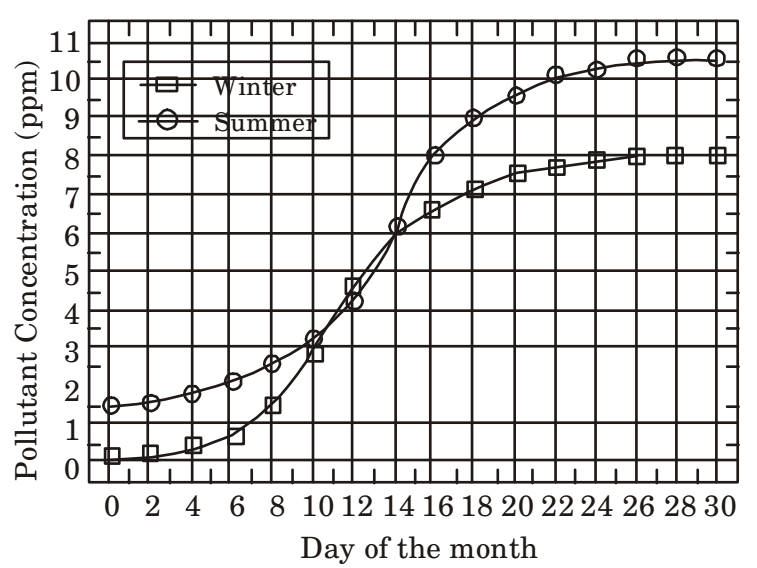
Consider the following statements based on the data shown above:
i. Over the given month, the difference between the maximum and the minimum pollutant concentrations is the same in both Winter and summer.
ii. There are at least four days in the summer month such that the pollutant concentrations on those days are within 1 ppm of the pollutant concentrations on the corresponding days in the Winter month. Which one of the following options is correct?
-
View Hint View Answer Discuss in Forum
NA
Correct Option: B
NA

