Numerical Ability
- What is the sum of the missing digits in the subtraction problem below?
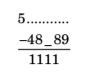
-
View Hint View Answer Discuss in Forum

Correct Option: D

- Let S1 be the plane figure consisting of the points (x, y) given by the inequalities |x –1| ≤ 2 and |y + 2| ≤ 3. Let S2 be the plane figure given by the inequalities x – y ≥ – 2, y ≥ 1, and x ≤ 3. Let S be the union of S1 and S2. The area of S is
-
View Hint View Answer Discuss in Forum

Correct Option: C

- The growth of bacteria (lactobacillus) in milk leads to curd formation. A minimum bacterial population density of 0.8 (in suitable) is needed to form curd. In the graph below, the population density of lactobacillus in 1 litre of milk is plotted as a function of time, at two different temperature, 25°C and 37°C.

Consider the following statements based on the data shown above:
i. The growth in bacterial population stops earlier at 37°C as compared to 25°C
ii. The time taken for curd formation at 25°C is twice the time taken at 37°C Which one of the following options is correct?
-
View Hint View Answer Discuss in Forum
I is true as very obvious from the given graph. II is false as the given graph shown only bacterial growth in milk but curd formation in milk may have other factors too like the purity of milk which might affect the speed of curd formation so II is false.
Hence, (a) is the correct answer.Correct Option: A
I is true as very obvious from the given graph. II is false as the given graph shown only bacterial growth in milk but curd formation in milk may have other factors too like the purity of milk which might affect the speed of curd formation so II is false.
Hence, (a) is the correct answer.
- If a and b are integers and a – b is even, which of the following must always be even?
-
View Hint View Answer Discuss in Forum
As a – b is even so a and b will be both even or both odd. Hence, option (d) will be the right answer.
Correct Option: D
As a – b is even so a and b will be both even or both odd. Hence, option (d) will be the right answer.
- P looks at Q while Q looks at R, P is married, R is not. The number of pairs of people in which a married person is looking at an unmarried person is
-
View Hint View Answer Discuss in Forum
NA
Correct Option: B
NA

