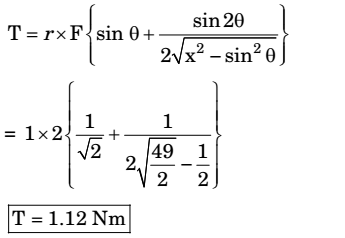Theory of Machines Miscellaneous

Theory of Machines Miscellaneous

Easy Questions
Moderate Questions
Difficult Questions

Theory of Machines

Theory of Machines Miscellaneous

Direction: A planetary gear train has four gears and one carrier. Angular velocities of the gears are ω1, ω2, ω3, and ω4, respectively. The carrier rotates with angular velocity ω5

  1. For ω1 = 60 rpm clockwise (cw) when viewed from the left, what is the angular velocity of the carrier and its direction. so that Gear 4 rotates in counter clockwise (ccw) direction at twice the angular velocity of Gear 1 when viewed from the left?








  1. View Hint View Answer Discuss in Forum

    156 rpm, ccw

    Correct Option: D

    156 rpm, ccw

  1. What is the relation between the angular velocities of Gear 1 and Gear 4?








  1. View Hint View Answer Discuss in Forum

    ω1 - ω5
    		= 3
    ω2 - ω5

    (with respect to arm 5 or carrier 5)
    ω3 - ω5
    		= 2
    ω4 - ω5

    (with respect to carrier 5)
    As ω3 = ω2
    ∴
    ω1 - ω5
    		= 6
    ω4 - ω5

    Correct Option: A

    ω1 - ω5
    		= 3
    ω2 - ω5

    (with respect to arm 5 or carrier 5)
    ω3 - ω5
    		= 2
    ω4 - ω5

    (with respect to carrier 5)
    As ω3 = ω2
    ∴
    ω1 - ω5
    		= 6
    ω4 - ω5

  1. The arm OA of a epicyclic gear train shown in figure revolves counter clockwise about Owith an angular velocity of 4 rad/s. Both gear are of same size. The angular velocity of gears C, if the sun gear B is fixed is








  1. View Hint View Answer Discuss in Forum


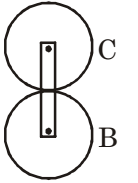
    Given: y = – 4 [CCW]
    N + y = 0 [Sun gear B is fixed]
    ∴ N = – y
    = 4 rad/sec
    Speed of gear C = – 4 – 4 = – 8 rad/sec

    Correct Option: B


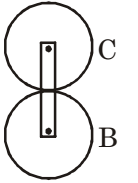
    Given: y = – 4 [CCW]
    N + y = 0 [Sun gear B is fixed]
    ∴ N = – y
    = 4 rad/sec
    Speed of gear C = – 4 – 4 = – 8 rad/sec

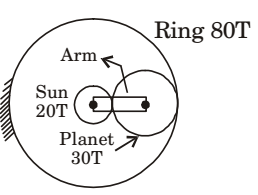
  1. The sun gear in the figure is driven clockwise at 100 rpm. The ring gear is held stationary. For the number of teeth shown on the gears, the arm rotates at








  1. View Hint View Answer Discuss in Forum


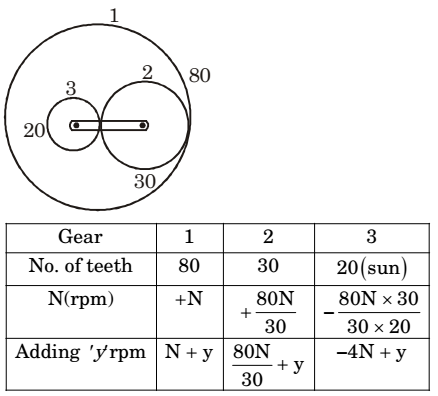
    Given: N + y = 0
    y = – N
    Sun gear means ‘‘3’’

    - N × 80 × 30
    		+ y =0
    30 × 20

    – 4N – N = 100
    – 5N = 100 N = – 20
    ∴ y = – N = + 20 rpm

    Correct Option: B


    Given: N + y = 0
    y = – N
    Sun gear means ‘‘3’’

    - N × 80 × 30
    		+ y =0
    30 × 20

    – 4N – N = 100
    – 5N = 100 N = – 20
    ∴ y = – N = + 20 rpm

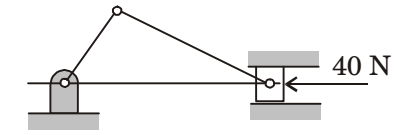
  1. A slider crank mechanism is shown in the figure. At some instant, the crank angle is 45° and a force of 40 N is acting towards the left on the slider. The length of the crank is 30 mm and the connecting rod is 70 mm. Ignoring the effect of gravity, friction and inertial forces, the magnitude of the crankshaft torque (in Nm) needed to keep the mechanism in equilibrium is _________ (correct to two decimal places).








  1. View Hint View Answer Discuss in Forum


    The Torque required to hold the mechanism in equilibrium is equal & opposite of turning moment.

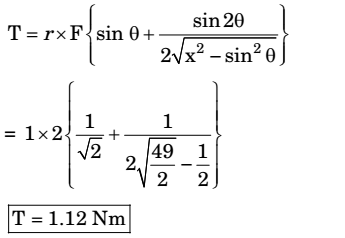
    Correct Option: C


    The Torque required to hold the mechanism in equilibrium is equal & opposite of turning moment.