Laws of Motion

Laws of Motion

Easy Questions
Moderate Questions
Difficult Questions

Mechanics

Physical World, Units and Measurements
Motion in a Straight Line
Motion in a Plane
Laws of Motion
Work, Energy and Power
Gravitation
Mechanical Properties of Solids
Mechanical Properties of Fluids
System of Particles and Rotational Motion
  1. A person of mass 60 kg is inside a lift of mass 940 kg and presses the button on control panel. The lift starts moving upwards with an acceleration  1.0 m/s². If g = 10 ms–2, the tension in the supporting cable is








  1. View Hint View Answer Discuss in Forum


    Total mass = (60 + 940) kg = 1000 kg
    Let T be the tension in the supporting cable, then
    T – 1000g = 1000 × 1
    ⇒ T = 1000 × 11 = 11000 N

    Correct Option: C


    Total mass = (60 + 940) kg = 1000 kg
    Let T be the tension in the supporting cable, then
    T – 1000g = 1000 × 1
    ⇒ T = 1000 × 11 = 11000 N


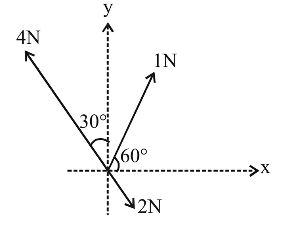
  1. Three forces acting on a body are shown in the figure. To have the resultant force only along the y- direction, the magnitude of the minimum additional force needed is:








  1. View Hint View Answer Discuss in Forum

    The components of 1 N and 2N forces along + x axis = 1 cos 60° + 2 sin 30°

    = 1'
    1
    		 + 2'
    1
    		 =
    1
    		 + 1 =
    3
    		 =1.5 N
    2222


    The component of 4 N force along –x-axis = 4 sin 30°
    = 4 ×
    1
    		 = 2N
    2

    Therefore, if a force of 0.5N is applied along + x-axis, the resultant force along x-axis will become zero and the resultant force will be obtained only along y-axis.

    Correct Option: A

    The components of 1 N and 2N forces along + x axis = 1 cos 60° + 2 sin 30°

    = 1'
    1
    		 + 2'
    1
    		 =
    1
    		 + 1 =
    3
    		 =1.5 N
    2222


    The component of 4 N force along –x-axis = 4 sin 30°
    = 4 ×
    1
    		 = 2N
    2

    Therefore, if a force of 0.5N is applied along + x-axis, the resultant force along x-axis will become zero and the resultant force will be obtained only along y-axis.

  1. The mass of a lift is 2000 kg. When the tension in the supporting cable is 28000 N, then its acceleration is:​​








  1. View Hint View Answer Discuss in Forum

    Net force, F = T – mg
    ma = T – mg
    2000 a = 28000 – 20000 = 8000

    a =
    8000
    		 = 4ms-2
    2000

    Correct Option: A

    Net force, F = T – mg
    ma = T – mg
    2000 a = 28000 – 20000 = 8000

    a =
    8000
    		 = 4ms-2
    2000

  1. The coefficient of static friction, µs, between block A of mass 2 kg and the table as shown in the figure is 0.2. What would be the maximum mass value of block B so that the two blocks do not move? The string and the pulley are assumed to be smooth and massless.
    (g = 10 m/s²) [2004]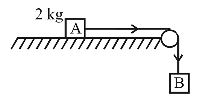








  1. View Hint View Answer Discuss in Forum

    mBg = µs mAg {∵ mAg = µs mAg}
    ⇒ mB = µs mA
    or, mB = 0.2 × 2 = 0.4 kg

    Correct Option: A

    mBg = µs mAg {∵ mAg = µs mAg}
    ⇒ mB = µs mA
    or, mB = 0.2 × 2 = 0.4 kg