31. If moist air is cooled by sensible heat removal, which of the following is true?

1. 1. Neither relative humidity nor specific humidity changes

   
   
   

   2. Specific humidity changes but not relative humidity

   
   
   

   3. Both relative humidity and specific humidity change

   
   
   

   4. None of these

   
   
   

---

1. View Hint View Answer Discuss in Forum

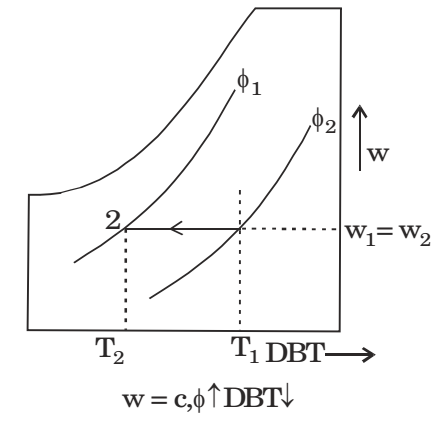
   Sensible cooling process
   

   Correct Option: D

   Sensible cooling process
   

---

32. Atmospheric air from 40°C and 60 percent relative humidity can be brought to 20°C and 60 percent relative humidity by

1. 1. Cooling and dehumidification process

   
   
   

   2. Cooling and humidification process

   
   
   

   3. Adiabatic saturation process

   
   
   

   4. Sensible cooling process

   
   
   

---

1. View Hint View Answer Discuss in Forum

   Cooling and dehumidification process,
   

   Correct Option: A

   Cooling and dehumidification process,
   

---

---

33. A reversed Carnot cycle refrigerator maintains a temperature of –5°C. The ambient air temperature is 35°C. The heat gained by the refrigerator at a continuous rate is 2.5 kJ/s. The power (in watt) required to pump this heat out continuously is _______

1. 1. 373.13

   
   
   

   2. 373.23

   
   
   

   3. 373

   
   
   

   4. 473.13

   
   
   

---

1. View Hint View Answer Discuss in Forum

   	Q1	=	Q2
   	268		308

   
   

   Q2 =	2.5 × 308	[Q1 = 2.5]
   	268

   
   Q₂ = 2.873 kW
   w = Q₂ – Q₁ = 0.373 kw = 373.13 Watt.

   Correct Option: A

   	Q1	=	Q2
   	268		308

   
   

   Q2 =	2.5 × 308	[Q1 = 2.5]
   	268

   
   Q₂ = 2.873 kW
   w = Q₂ – Q₁ = 0.373 kw = 373.13 Watt.

---

34. A thin layer of water in a field is formed after a farmer has watered it. The ambient air conditions are: temp. 20°C and relative humidity 5%. An extract of steam tables is given below.
    
    Neglecting the heat transfer between the water and the ground, the water temperature in the field after phase equilibrium is reached equals

1. 1. 10.3°C

   
   
   

   2. –10.3°C

   
   
   

   3. –14.5°C

   
   
   

   4. 14.5°C

   
   
   

---

1. View Hint View Answer Discuss in Forum

   Given data:
   Φ = 5% = 0.05
   T_db = 20°C
   From table
   At 20°C, P_s = 2.34 kPa
   

   Φ =	Pv
   	Ps

   
   

   0.05 =	Pv
   	2.34

   
   P_v =.117 k Pa By Interpolation method,
   

   Tdb = - 15 +	(-10 + 15	× (0.117 - .1)
   	0.26 - 0.10

   
   = – 15 + 0.531 = – 14.5° C

   Correct Option: C

   Given data:
   Φ = 5% = 0.05
   T_db = 20°C
   From table
   At 20°C, P_s = 2.34 kPa
   

   Φ =	Pv
   	Ps

   
   

   0.05 =	Pv
   	2.34

   
   P_v =.117 k Pa By Interpolation method,
   

   Tdb = - 15 +	(-10 + 15	× (0.117 - .1)
   	0.26 - 0.10

   
   = – 15 + 0.531 = – 14.5° C

---

---

35. A heat engine having an efficiency of 70% is used to drive a refrigerator having a coefficient of performance of 5. The energy absorbed from low temperature reservoir by the refrigerator for each kJ of energy absorbed from high temperature source by the engine is

1. 1. 0.14kJ

   
   
   

   2. 0.71kJ

   
   
   

   3. 3.5 kJ

   
   
   

   4. 7.1 kJ

   
   
   

---

1. View Hint View Answer Discuss in Forum

   Given: η_engine = 0.7, (C.O.P)_R = 5
   

   ηengine =	W	...(i)
   	Q1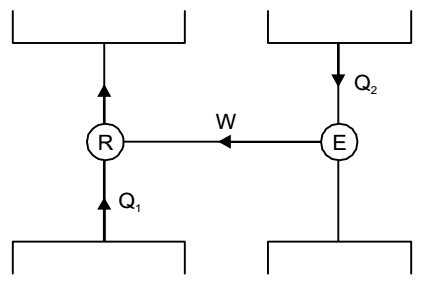

   
   
   Now,
   

   (C.O.P)R =	Q2
   	W

   
   

   ∴ W =	Q2	...(ii)
   	5

   
   Again,
   

   0.7 =	Q2	×	1
   	5		Q1

   
   

   or	Q2	= 3.5
   	Q1

   
   Energy absorbed from low temperature reservoir by the refrigerator for each kJ of energy absorbed from high temperature source by the engine = 3.5 kJ.

   Correct Option: C

   Given: η_engine = 0.7, (C.O.P)_R = 5
   

   ηengine =	W	...(i)
   	Q1

   
   
   Now,
   

   (C.O.P)R =	Q2
   	W

   
   

   ∴ W =	Q2	...(ii)
   	5

   
   Again,
   

   0.7 =	Q2	×	1
   	5		Q1

   
   

   or	Q2	= 3.5
   	Q1

   
   Energy absorbed from low temperature reservoir by the refrigerator for each kJ of energy absorbed from high temperature source by the engine = 3.5 kJ.

---