Laws of Motion
- A 5000 kg rocket is set for vertical firing. The exhaust speed is 800 ms–1. To give an initial upward acceleration of 20 ms–2, the amount of gas ejected per second to supply the needed thrust will be (g = 10 ms–2)
-
View Hint View Answer Discuss in Forum
Given : Mass of rocket (m) = 5000 kg
Exhaust speed (v) = 800 m/s
Acceleration of rocket (a) = 20 m/s²
Gravitational acceleration (g) = 10 m/s²
We know that upward force
F = m (g + a) = 5000 (10 +20)
= 5000 × 30 = 150000 N.
We also know that amount of gas ejected
dm 
= F = 150000 = 187.5 kg/s dt v 800 Correct Option: B
Given : Mass of rocket (m) = 5000 kg
Exhaust speed (v) = 800 m/s
Acceleration of rocket (a) = 20 m/s²
Gravitational acceleration (g) = 10 m/s²
We know that upward force
F = m (g + a) = 5000 (10 +20)
= 5000 × 30 = 150000 N.
We also know that amount of gas ejected
dm 
= F = 150000 = 187.5 kg/s dt v 800
- A bullet is fired from a gun. The force on the bullet is given by F = 600 – 2 × 105 t where, F is in newton and t in second. The force on the bullet becomes zero as soon as it leaves the barrel. What is the average impulse imparted to the bullet?
-
View Hint View Answer Discuss in Forum
Given F = 600 - (2 &time; 105t)
The force is zero at time t, given by⇒ t = 600 = 3 × 10-3 second 2 &time; 105 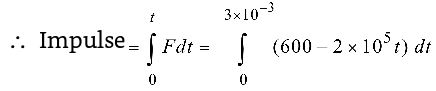
= 
600t - 2 × 105t² 
3 × 10-3 2 0
= 300 &time; 3 &time; 10-3 - 105(3 × 10-3)²
= 1.8 - 0.9 = 0.9NsCorrect Option: D
Given F = 600 - (2 &time; 105t)
The force is zero at time t, given by⇒ t = 600 = 3 × 10-3 second 2 &time; 105 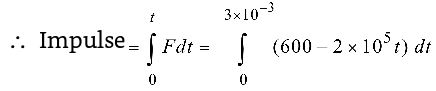
= 
600t - 2 × 105t² 
3 × 10-3 2 0
= 300 &time; 3 &time; 10-3 - 105(3 × 10-3)²
= 1.8 - 0.9 = 0.9Ns
- If a cricketer catches a ball of mass 150 gm moving with a velocity of 20 m/s, then he experiences a force of (Time taken to complete the catch is 0.1 sec.)
-
View Hint View Answer Discuss in Forum
Net force experienced = Total impulse Time taken = mΔv = 0.15 × 20 = 30N t 0.1 Correct Option: B
Net force experienced = Total impulse Time taken = mΔv = 0.15 × 20 = 30N t 0.1
- The force ‘F’ acting on a particle of mass ‘m’ is indicated by the force-time graph shown below. The change in momentum of the particle over the time interval from zero to 8 s is :[2014]
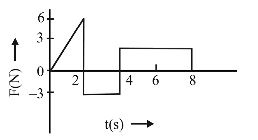
-
View Hint View Answer Discuss in Forum
Change in momentum,
∆p= ∫Fdt
= Area of F-t graph
= ar of ∆ – ar of ☐ + ar of ☐= 1 &time; 2 × 6 - 3 × 2 + 4 × 3 = 12 N-s 2 Correct Option: C
Change in momentum,
∆p= ∫Fdt
= Area of F-t graph
= ar of ∆ – ar of ☐ + ar of ☐= 1 &time; 2 × 6 - 3 × 2 + 4 × 3 = 12 N-s 2

