16. In the case of turbulent flow of a fluid though a circular tube (as compared to the case of laminar flow at the same flow rate) the maximum velocity is _________shear stress at the wall is _______, and the pressure drop across a given length is __________ The correct words for the blanks are, respectively

1. 1. higher, higher, higher

   
   
   

   2. higher, lower, lower

   
   
   

   3. lower, higher, higher

   
   
   

   4. lower, higher, lower

   
   
   

---

1. View Hint View Answer Discuss in Forum

   NA

   Correct Option: C

   NA

---

17. Prandtl's mixing length in turbulent flow signifies

1. 1. the average distance perpendicular to the mean flow covered by the mixing particles

   
   
   

   2. the ratio of mean free path to characteristic length of the flow field

   
   
   

   3. the wavelength corresponding to the lowest frequency present in the flow field

   
   
   

   4. the magnitude of turbulent kinetic energy

   
   
   

---

1. View Hint View Answer Discuss in Forum

   NA

   Correct Option: A

   NA

---

---

18. Match the following
    

    P: Compressible flow	U: Reynolds number
    Q: Free surface flow	V: Nusselt number
    R: Boundary layer flow	W:Weber number
    S: Pipe flow	X: Froude number
    T: Heat convection	Y: Mach number
    Z: Skin friction coefficient

1. 1. P-U; Q-X; R-V; S-Z; T-W

   
   
   

   2. P-W; Q-X; R-Z; S-U; T-V

   
   
   

   3. P-Y; Q-W; R-Z; S-U; T-X

   
   
   

   4. P-Y; Q-X; R-Z; S-U; T-V

   
   
   

---

1. View Hint View Answer Discuss in Forum

   NA

   Correct Option: D

   NA

---

19. Consider the turbulent flow of a fluid through a circular pipe of diameter D.Identify the correct pair of statements. I. The fluid is well-mixed
    II. The fluid is unmixed
    III.Re_D < 2300
    IV. Re_D > 2300

1. 1. I and III

   
   
   

   2. II and IV

   
   
   

   3. II and III

   
   
   

   4. I and IV

   
   
   

---

1. View Hint View Answer Discuss in Forum

   Re_D > 2300 means it is a turbulent flow. I n turbulent flow, the fluid is well mixed. The fluid is unmixed, for a very-low Reynolds number laminar flow.

   Correct Option: D

   Re_D > 2300 means it is a turbulent flow. I n turbulent flow, the fluid is well mixed. The fluid is unmixed, for a very-low Reynolds number laminar flow.

---

---

20. For a fluid flow through a divergent pipe of length L having inlet and outlet radii of R₁, and R₂ respectively and a constant flow rate of Q, assuming the velocity to be axial and uniform at any cross-section, the acceleration at the exit is

1. 1. 2Q(R1 - R2)

      πLR³2

   
   
   

   2. 2Q²(R1 - R2)

      π²LR³2

   
   
   

   3. 2Q²(R1 - R2)

      π²LR52

   
   
   

   4. 2Q²(R2 - R1)

      π²LR52

   
   
   

---

1. View Hint View Answer Discuss in Forum

   Velocity at inlet,
   

   u1 =	Q
   	πR²1

   
   Velocity at outlet,
   

   u2 =	Q
   	πR²2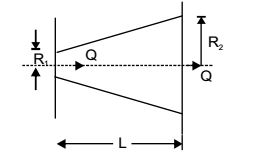

   
   
   

   Acceleration =	v.du
   	dx

   
   

   ∴	du	=	u2 - u1	=	Q		R²1	-	R²2
   	dx		L		πL		R²2		R²1

   
   

   Acceleration at the exit = u2.	dv
   	dx

   
   

   =	Q		Q		R²1 - R²2
   	πR²2		πL		R²1 R²2

   
   

   =	Q²		(R1 - R2)(R1 + R2)
   	π²R²1L		R²1 R²2

   
   Consider limiting case, i.e. R₁ → R₂, we have
   

   Acceleration at the exit =	Q²
   	π²R²LL

   
   

   h = x		(R1 - R2)(R1 + R2)		=	2Q²(R1 - R2)
   		R42			π²R52L

   Correct Option: C

   Velocity at inlet,
   

   u1 =	Q
   	πR²1

   
   Velocity at outlet,
   

   u2 =	Q
   	πR²2

   
   
   

   Acceleration =	v.du
   	dx

   
   

   ∴	du	=	u2 - u1	=	Q		R²1	-	R²2
   	dx		L		πL		R²2		R²1

   
   

   Acceleration at the exit = u2.	dv
   	dx

   
   

   =	Q		Q		R²1 - R²2
   	πR²2		πL		R²1 R²2

   
   

   =	Q²		(R1 - R2)(R1 + R2)
   	π²R²1L		R²1 R²2

   
   Consider limiting case, i.e. R₁ → R₂, we have
   

   Acceleration at the exit =	Q²
   	π²R²LL

   
   

   h = x		(R1 - R2)(R1 + R2)		=	2Q²(R1 - R2)
   		R42			π²R52L

---