Fluid Mechanics and Hydraulic Machinery Miscellaneous
- Figure shows the schematic for the measurement of velocity of air (density = 1.2 kg/m³) through a constant-area duct using a pitot tube and a water tube manometer. The differential head of water (density = 1000 kg/ m³) in the two columns of the manometer is 10 mm. Take acceleration due to gravity as 9.8 m/s². The velocity of air in m/s is 10 m m

-
View Hint View Answer Discuss in Forum
From Bernoulli's equation
v²1 - v²2 = p2 - p1 2g 2g ⇒ v1 = √ (p2 - p1) pa
But p2 - p1 = (ρgh)water
= 9810 × 10 × 10– 3
= 98.1 N/m²⇒ v1 = √ 2 × 98.1 = 12.8 m/s 1.2 Correct Option: C
From Bernoulli's equation
v²1 - v²2 = p2 - p1 2g 2g ⇒ v1 = √ (p2 - p1) pa
But p2 - p1 = (ρgh)water
= 9810 × 10 × 10– 3
= 98.1 N/m²⇒ v1 = √ 2 × 98.1 = 12.8 m/s 1.2
- Water (ρ = 1000 kg/m³) flows through a venturimeter with inlet diameter 80 mm and throat diameter 40 mm. The inlet and throat gauge pressures are measured to be 400 kPa and 130 kPa respectively. Assuming the venturimeter to be horizontal and neglecting friction, the inlet velocity (in m/s) is ________.
-
View Hint View Answer Discuss in Forum
p1 + v²1 = p2 + v²2 ρg 2g ρg 2g 
p1 = 400000 
p2 = 1300000
v1 × 80² = v2 × 40²
v2 = 4v1
Substituting v2 and solving for v1 we get v1 = 6m/sCorrect Option: D
p1 + v²1 = p2 + v²2 ρg 2g ρg 2g 
p1 = 400000 
p2 = 1300000
v1 × 80² = v2 × 40²
v2 = 4v1
Substituting v2 and solving for v1 we get v1 = 6m/s
- A horizontal - shaft centrifugal pump lifts water at 65°C.The suction nozzle is one meter below pump centerline. The pressure at this point equals 200 kPa gauge and velocity is 3 m/s. Steam tables show saturation pressure at 65°C is 25 kPa, and specific volume of the saturated liquid is 0.001020 m³/kg. The pump Net Positive Suction Head (NPSH) in meters is
-
View Hint View Answer Discuss in Forum
Given data:
Temperature of water,
T = 65°C Section head,
hs = 1m
Gauga pressure at section inlet,
p1.g = 200 kPa
∴ Absolute pressure,
P1.abs = P1.g + Patm
= 200 + 101.325
= 301.325 kPa
= 301.325 × 10³ pa
Velocity at section nozzle inlet,
V1 = 3 m/s
Saturated pressure at 65°C,
Pv.abs = 25 kPa, vapour pressure
= 25 × 10³ Pa
Specific volume,
V = 0.001020 m³/kg
Specific volume,
V = 0.001020 m³/kg∴ Density: ρ = 1 = 980.39 kg/m³ 0.001020 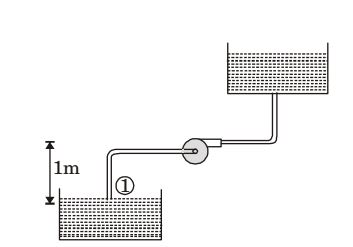
Net Positive Section Head
Net positive section head,NPSH = PS,abs + V²s - Pv.abs ρg 2g ρg
Applying Bernoulli’s equation at section nozzle inlet and section of the pumpP1.abs + V²1 + Ps.abs + V²s + hs ρg 2g ρg 2g P1.abs + V² + 0 = Ps.abs + V²s + hs ρg 2g ρg 2g or Ps.abs + V²s + Pt.abs + V²1 - hs ρg 2g ρg 2g ∴ NPSH = Ps.abs + V²s - hs Pv.abs ρg 2g ρg = 301.325 × 10³ + (3)² - 1 - 25 × 10³ 980.39 × 9.81 2 × 9.81 980.39 × 9.81
= 31.33 + 0.45 – 0.45–1 – 2.56
= 28.22m = 28 mCorrect Option: C
Given data:
Temperature of water,
T = 65°C Section head,
hs = 1m
Gauga pressure at section inlet,
p1.g = 200 kPa
∴ Absolute pressure,
P1.abs = P1.g + Patm
= 200 + 101.325
= 301.325 kPa
= 301.325 × 10³ pa
Velocity at section nozzle inlet,
V1 = 3 m/s
Saturated pressure at 65°C,
Pv.abs = 25 kPa, vapour pressure
= 25 × 10³ Pa
Specific volume,
V = 0.001020 m³/kg
Specific volume,
V = 0.001020 m³/kg∴ Density: ρ = 1 = 980.39 kg/m³ 0.001020 
Net Positive Section Head
Net positive section head,NPSH = PS,abs + V²s - Pv.abs ρg 2g ρg
Applying Bernoulli’s equation at section nozzle inlet and section of the pumpP1.abs + V²1 + Ps.abs + V²s + hs ρg 2g ρg 2g P1.abs + V² + 0 = Ps.abs + V²s + hs ρg 2g ρg 2g or Ps.abs + V²s + Pt.abs + V²1 - hs ρg 2g ρg 2g ∴ NPSH = Ps.abs + V²s - hs Pv.abs ρg 2g ρg = 301.325 × 10³ + (3)² - 1 - 25 × 10³ 980.39 × 9.81 2 × 9.81 980.39 × 9.81
= 31.33 + 0.45 – 0.45–1 – 2.56
= 28.22m = 28 m
- For the laminar flow of water oyer a sphere, the drag coefficient CF is defined as CF = F/(ρU²D²), where F is the drag force, ρ is the fluid density, U is the fluid velocity and D is the diameter of the sphere. The density of water is 1000 kg/m³. When the diameter of the sphere is 100 mm and the fluid velocity is 2 m/ s, the drag coefficient is 0.5. If water now flows over another sphere of diameter 200 mm under dynamically similar conditions, the drag force (in N) on this sphere is _______.
-
View Hint View Answer Discuss in Forum
Drag coefficient,
Cf = F ρU²D²
F = CfρU²D²
For sphere –1
ρ1 = 1000 kg/m³
D1 = 100 mm = 0.1m
U1 = 2 m/s
CF = 0.5
For sphere –2
ρ2 = 1000 kg/m²
But D2 = 0.2m
Due to dynamically similar conditions:
(Re)1 = (Re)2U1D1 = U2D2 v1 v2
2 × 0.1 = U2 × 0.2
U2 = 1 m/s
F2 = CFρU²2D²2
F2 = 0.5 × 1000 × 1² × 2²
= 20NCorrect Option: C
Drag coefficient,
Cf = F ρU²D²
F = CfρU²D²
For sphere –1
ρ1 = 1000 kg/m³
D1 = 100 mm = 0.1m
U1 = 2 m/s
CF = 0.5
For sphere –2
ρ2 = 1000 kg/m²
But D2 = 0.2m
Due to dynamically similar conditions:
(Re)1 = (Re)2U1D1 = U2D2 v1 v2
2 × 0.1 = U2 × 0.2
U2 = 1 m/s
F2 = CFρU²2D²2
F2 = 0.5 × 1000 × 1² × 2²
= 20N
- Water enters a circular pipe of length L = 5.0 m and diameter D = 0.20 m with Reynolds number ReD = 500. The velocity profile at the inlet of the pipe is uniform while it is parabolic at the exit. The Reynolds number at the exit of the pipe is_____
-
View Hint View Answer Discuss in Forum
Since discharge is not changing average velocity in constant dia pipe will not change
Re = ρVD μ
Reynold’s no. will not change
Re at exit = 500Correct Option: B
Since discharge is not changing average velocity in constant dia pipe will not change
Re = ρVD μ
Reynold’s no. will not change
Re at exit = 500

