-
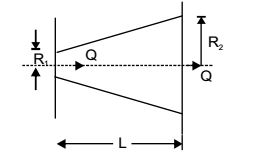
For a fluid flow through a divergent pipe of length L having inlet and outlet radii of R1, and R2 respectively and a constant flow rate of Q, assuming the velocity to be axial and uniform at any cross-section, the acceleration at the exit is
-
-
2Q(R1 - R2) πLR³2 -
2Q²(R1 - R2) π²LR³2 -
2Q²(R1 - R2) π²LR52 -
2Q²(R2 - R1) π²LR52
-
Correct Option: C
Velocity at inlet,
| u1 = | ||
| πR²1 |
Velocity at outlet,
| u2 = | ||
| πR²2 |
| Acceleration = | ||
| dx |
| ∴ | = | = |  | - |  | |||||
| dx | L | πL | R²2 | R²1 |
| Acceleration at the exit = u2. | ||
| dx |
| = |  |  |  |  | |||
| πR²2 | πL | R²1 R²2 |
| = |  |  | ||
| π²R²1L | R²1 R²2 |
Consider limiting case, i.e. R1 → R2, we have
| Acceleration at the exit = | ||
| π²R²LL |
| h = x |  |  | = | ||
| R42 | π²R52L |

