Electronic measurements and instrumentation miscellaneous Difficult Questions and Answers | Page - 4

Electronic measurements and instrumentation miscellaneous

A 0–25A ammeter has a guaranteed accuracy of 1 per cent of full scale reading. The current measured by this instrument is 5A. The limiting error in percentage will be:

1. 1%
1. 5%
1. 10%
1. 25%

View Hint View Answer Discuss in Forum

Given ammeter range 0 – 25A
relative error = E_r = 1% = 0·01
The magnitude of limiting error of the instrument
δA = E_r × A where, A is the true value
= 0·01 × 25
= 0·25A
The magnitude of the current being measured is 5.
The relative error at this current is
E_r = δA = 0.25 = 0.05
A 5

or
percentage relative or limiting error = 5%.

Correct Option: B

Given ammeter range 0 – 25A
relative error = E_r = 1% = 0·01
The magnitude of limiting error of the instrument
δA = E_r × A where, A is the true value
= 0·01 × 25
= 0·25A
The magnitude of the current being measured is 5.
The relative error at this current is
E_r = δA = 0.25 = 0.05
A 5

or
percentage relative or limiting error = 5%.

As compared to other voltmeters the digital voltmeter offer the advantage of:

1. greater speed
1. higher accuracy and resolution
1. reduced human error
1. all of the above

View Hint View Answer Discuss in Forum

As compared to other voltmeter the digital voltmeter offers the advantage of:
● Greater speed
● Higher accuracy and resolution
● Less human error

Correct Option: D

As compared to other voltmeter the digital voltmeter offers the advantage of:
● Greater speed
● Higher accuracy and resolution
● Less human error

Which of the following conditions are to be satisfied in the figure shown, so that the common variable shaft of resistance R₁ and R₂ can be graduated in frequency to measure the frequency of E under balanced condition?
1. R₁ = R₃
2. C₁ = C₃
3. R₂ = 2 R₄
4. R₂ = R₄
Select the correct answer using the codes given below: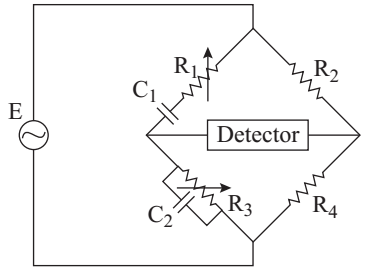

1. 1 and 4
1. 1 and 2
1. 2 and 4
1. 1, 2 and 3

View Hint View Answer Discuss in Forum

Under the balanced condition.
From above figure
R₁ + 1 / 2 = R₃ 1/j_ωC₃ × 1
1/j_ωC₁ R₁ +(1/j_ωC₃) R₃

or
R₄ R₁ + 1 = R₂ R₃
j_ωC₁ jR_3ωC₃₊₁

or R₄ [jR_1ωC₁₊₁] [1 + j_ωC₃R₃]=j_ωC₁R₂R₃
on comparing real and imaginary part, we get,
R₁R₃C_2ω = 1
c_1ω

or
ω² = 1
C₁C₃R₁R₃

or
ω = 1
√C₁C₃R₁R₃

If C₁ = C₃
and R₁ = R₃
then given R₂ = 2R₄
Thus condition to be satisfied are
C₁ = C₃, R₁ = R₃
and R₂ = 2R₄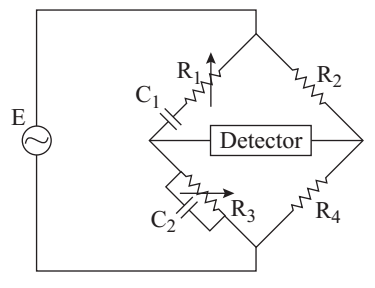

Correct Option: D

Under the balanced condition.
From above figure
R₁ + 1 / 2 = R₃ 1/j_ωC₃ × 1
1/j_ωC₁ R₁ +(1/j_ωC₃) R₃

or
R₄ R₁ + 1 = R₂ R₃
j_ωC₁ jR_3ωC₃₊₁

or R₄ [jR_1ωC₁₊₁] [1 + j_ωC₃R₃]=j_ωC₁R₂R₃
on comparing real and imaginary part, we get,
R₁R₃C_2ω = 1
c_1ω

or
ω² = 1
C₁C₃R₁R₃

or
ω = 1
√C₁C₃R₁R₃

If C₁ = C₃
and R₁ = R₃
then given R₂ = 2R₄
Thus condition to be satisfied are
C₁ = C₃, R₁ = R₃
and R₂ = 2R₄

Match List-I with List-II and select the correct answer using the codes given below the Lists:

List-I	List-II
A. Meggar	1. Measurement of loss angle in a dielectric.
B. Spectrum analyzer	2. Measurement of frequency.
C. Schering bridge	3. Measurement of insulation resistance.
D. Digital counter	4. Measurement of harmonics.

1. A B C D
  1 2 3 4
1. A B C D
  1 2 4 3
1. A B C D
  4 3 2 1
1. A B C D
  3 4 1 2

View Hint View Answer Discuss in Forum

● Meggar → Measurement of insulation resistance
● Spectrum analyzer → Measurement of harmonics
● Schering bridge → Measurement of loss angle in a dielectric
● Digital counter → Measurement of frequency

Correct Option: D

● Meggar → Measurement of insulation resistance
● Spectrum analyzer → Measurement of harmonics
● Schering bridge → Measurement of loss angle in a dielectric
● Digital counter → Measurement of frequency

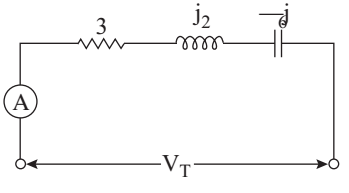
In the ac circuit shown in the given figure, when the ammeter reads 10A, the readings on a voltmeter placed across the entire circuit and then across each element are given below. Match List-I (Position of the voltmeter) with List-II (readings on the voltmeter) and select the correct answer using the codes given below the list:
List-I List-II
A. VT 1. 60
B. VR 2. 20
C. VL 3. 30
D. VC 4. 50
5. 110

A B C D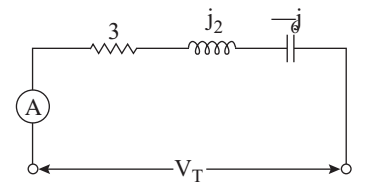

1. A B C D
  5 4 2 1
1. A B C D
  5 3 1 2
1. A B C D
  4 5 1 2
1. A B C D
  4 3 2 1

View Hint View Answer Discuss in Forum

Given, I = 10A
R = 3Ω
X_L = j2Ω
X_C = – j6Ω
V_R = IR = 10 × 3 = 30V
V_L = IX_L = 10 × 2 = 20V
V_C = IX_C = 10 × 6 = 60V
V_T = √V_R² + (V_L ~ V_C)²
or
V_T = √30² + (60 – 20)²
or
V_T = √30² + 40²
or
V_T = 50
Finally →

V_T = 50V
V_R = 30V
V_L = 20V
V_c = 60V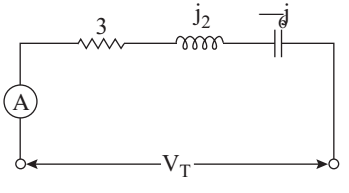

Correct Option: D

Given, I = 10A
R = 3Ω
X_L = j2Ω
X_C = – j6Ω
V_R = IR = 10 × 3 = 30V
V_L = IX_L = 10 × 2 = 20V
V_C = IX_C = 10 × 6 = 60V
V_T = √V_R² + (V_L ~ V_C)²
or
V_T = √30² + (60 – 20)²
or
V_T = √30² + 40²
or
V_T = 50
Finally →

V_T = 50V
V_R = 30V
V_L = 20V
V_c = 60V