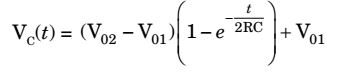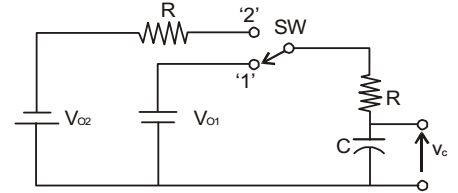
The switch SW shown in the circuit is kept at position ‘1’

Home » Electric Circuits » Electric circuits miscellaneous » Question

The switch SW shown in the circuit is kept at position ‘1’ for a long duration. At t = 0+, the switch is moved to position ‘2’. Assuming | Vo₂ | > | Vo₁ |, the voltage v_c (t) across the capacitor is

1. V_c(t) = -V_o2(1 - e^{-t / 2RC} - V_o1
2. V_c(t) = V_o2(1 - e^{-t / 2RC} + V_o1
3. V_c(t) = -(V_o2 + V_o1) (1 - e^{-t / 2RC} - V_o1
4. V_c(t) = (V_o2 - V_o1) (1 - e^{-t / 2RC} + V_o1

Correct Option: D

When the switch SW is at position 1, the capacitor C is charged to voltage V₀₁.
Now, when the switch SW is thrown to position 2, the circuit becomes as shown below :

V_C (0^-) = V_C (0⁺) = V₀₁
Using KVL in the circuit, we get

V₀₂ - 2R	dq	-	q	= 0
	dt		c

⇒	dq	=	dt
	cV₀₂ - q		2RC