Compiler design miscellaneous Easy Questions and Answers | Page - 8

Compiler design miscellaneous

The grammar S → aSa | bS| c is

1. LL (1) but not LR (1)
1. LR (1) but not LL (1)
1. Both LL (1) and LR (1)
1. Neither LL (1) and LR (1)

View Hint View Answer Discuss in Forum

S → aSa | bS | C
The above grammar is LL (1) because,
First [aSa] ∩ first [bS] = (a) ∩ (b) = φ
First [bS] ∩ first [c] = (b) ∩ (c) = φ
First [c] ∩ first [aSa] = (c) ∩ (a) = φ
As the above grammar is LL (1), also LR (1) because LL (1) grammar is always LR (1) grammar.

Correct Option: C

S → aSa | bS | C
The above grammar is LL (1) because,
First [aSa] ∩ first [bS] = (a) ∩ (b) = φ
First [bS] ∩ first [c] = (b) ∩ (c) = φ
First [c] ∩ first [aSa] = (c) ∩ (a) = φ
As the above grammar is LL (1), also LR (1) because LL (1) grammar is always LR (1) grammar.

For a C program accessing X[i][j][k], the following intermediate code is generated by a compiler. Assume that the size of an integer is 32 bits and the size of a character is 8 bits.
t0 = i * 1024
t1 = j * 32
t2 = k * 4
t3 = t1 + t0
t4 = t3 + t2
t5 = X[t4]
Which one of the following statements about the source code for the C program is

1. X is declared as “int X[32][32][8]”.
1. X is declared as “int X[4][1024][32]”.
1. X is declared as “char X[4][32][8]”.
1. X is declared as “char X[32][16][2]”.

View Hint View Answer Discuss in Forum

X is declared as “int × [32] [32] [8]”

Correct Option: A

X is declared as “int × [32] [32] [8]”

The least number of temporary variables required to create three-address code in static single assignment form for the expression q + r /3 + s – t*5 + u*v /w is ______.

1. 0
1. 3
1. 1
1. 2

View Hint View Answer Discuss in Forum

3

Correct Option: B

3

The secant method is used to find the root of an equation f(x) = 0. It is started from two distinct estimates x_a and x_b for the root. It is an iterative procedure involving linear interpolation to a root. The iteration stops if f(x_b) is very small and then x_b is the solution. The procedure is given below. Observe that there is an expression which is missing and is marked by? Which is the suitable expression that is to be put in place of?
So that it follows all steps of the secant method?
Secant
Initialize : x_a, x_b, ε , N
// ε = convergence indicator
// N = maximum number of iterations
f_b = f(x_b)
i = 0
while (i < N and |f_b | > ε ) do
i = i + 1// update counter
x_t =? // missing expression for
x_a = x_b
x_b = x_t // intermediate value
f_b = f(x_b) // function value at new x_b
end while
if |f_b | > ε then // loop is terminated with i = N
write "Non-convergence"
else
write "return x_b "
end if

1. x_b – (f_b – f(x_a)) f_b / (x_b – x_a)
1. x_a – (f_a – f(x_a)) f_a/ x_b– x_a)
1. x_b – (x_b – x_a )f_b / (f_b – f(x_a))
1. x_a – (x_b – x_a) f_a / (f_b – f(x_a))

View Hint View Answer Discuss in Forum

It is secant method direct formula.

Correct Option: D

It is secant method direct formula.

Consider the translation scheme shown below:
S → RT
R → + T {print (‘+’:) R/ ε
T → num {print (num. val);}
Here, num is a taken that represents an integer and num. val represents the corresponding integer value. For an input string ‘9 + 5 + 2’, this translation scheme will print

1. 9 + 5 + 2
1. 95 + 2 +
1. 952 + +
1. + + 952

View Hint View Answer Discuss in Forum

Let us make the parse tree for 9 + 5 + 2 in top down manner, left first derivation.
Steps:
1) Expand S → TR
2) Apply T → Num...
3) Apply R → +T...
4) Apply T → Num...
5) Apply R → +T..
6) Apply T → Num..
7) Apply R → ε (epsilon)
After printing through the print statement in the parse tree formed you will get the answer as 95 + 2 +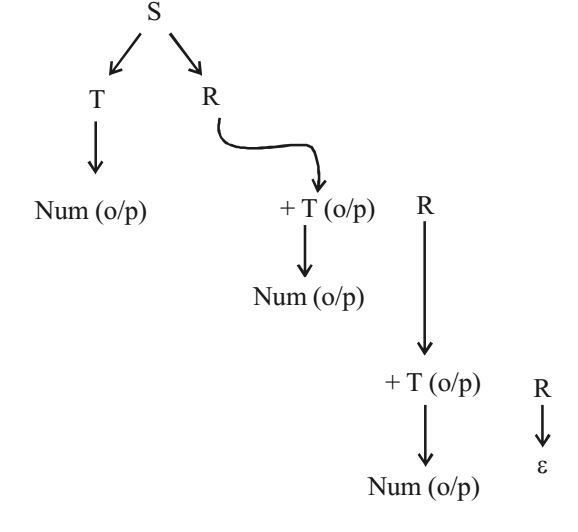

Correct Option: B

Let us make the parse tree for 9 + 5 + 2 in top down manner, left first derivation.
Steps:
1) Expand S → TR
2) Apply T → Num...
3) Apply R → +T...
4) Apply T → Num...
5) Apply R → +T..
6) Apply T → Num..
7) Apply R → ε (epsilon)
After printing through the print statement in the parse tree formed you will get the answer as 95 + 2 +