Compiler design miscellaneous

Compiler design miscellaneous

Easy Questions

Compiler Design

Compiler design miscellaneous
  1. Which of the following grammar rules violate the requirement of an operator grammar? P, Q, R are non – terminals, and r, s, t are terminals.
    1. P → Q R
    2. P → Q S R
    3. P → ε
    4. P → Q t R r








  1. View Hint View Answer Discuss in Forum

    1. P → QR is not possible since two NT should include one operator as Terminal.
    2. Correct
    3. Again incorrect.
    4. Correct.
    Hence (b) is correct option.

    Correct Option: B

    1. P → QR is not possible since two NT should include one operator as Terminal.
    2. Correct
    3. Again incorrect.
    4. Correct.
    Hence (b) is correct option.

  1. Consider the grammar rule E → E1 – E2 for arithmetic expressions. The code generated is targeted to a CPU having a single user register. The subtraction operation requires the first operand to be in the register. If E1 and E2 do not have any common sub-expression, in order to get shortest possible code.








  1. View Hint View Answer Discuss in Forum

    E1 is to be kept in accumulator & accumulator is required for operations to evaluate E2 also. So E2 should be evaluated first & then E1, so finally E1 will be in accumulator, otherwise need to use move & load instructions.
    Hence (b) is correct option.

    Correct Option: B

    E1 is to be kept in accumulator & accumulator is required for operations to evaluate E2 also. So E2 should be evaluated first & then E1, so finally E1 will be in accumulator, otherwise need to use move & load instructions.
    Hence (b) is correct option.

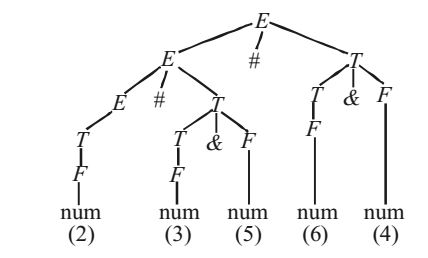
  1. Consider the grammar with the following translation rules and E as the start symbol:
    E → E #T {E. value = E1 value * T. value}
    | T {E. value = T. value}
    T → T1 & F {T. value = T1 value F. value}
    | F {T. value =F. value}
    F → num {F. value = num. value}
    Compute E value for the root ofthe parser tree for the expression
    2 # 3 & 5 # 6 & 4.








  1. View Hint View Answer Discuss in Forum

    The parse tree would be

    Now we evaluate bottom up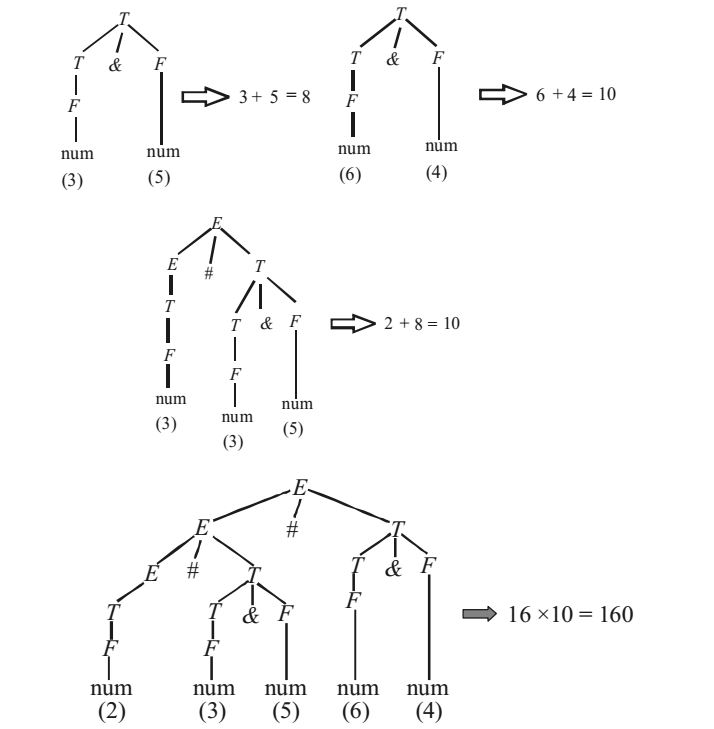

    LL " left to right left most derivation no ambignity should be there SLR or LR(0) L to R reverse right sentential form create LR(0) items. CLR or LR(1) create LR(1) items no bound LALR reduced CLR if while reducing any conflict found then not LALR Hence (c) is correct option.

    Correct Option: D

    The parse tree would be

    Now we evaluate bottom up

    LL " left to right left most derivation no ambignity should be there SLR or LR(0) L to R reverse right sentential form create LR(0) items. CLR or LR(1) create LR(1) items no bound LALR reduced CLR if while reducing any conflict found then not LALR Hence (c) is correct option.

  1. The grammar A → AA | (A) | ∈ is not suitable for predictive parsing because the grammar is








  1. View Hint View Answer Discuss in Forum

    Grammar is left recursive, hence the predictive parser may fall into a infinite loop. Answer A is not correct because ambiguity can occur from both left and right recursion.

    Correct Option: B

    Grammar is left recursive, hence the predictive parser may fall into a infinite loop. Answer A is not correct because ambiguity can occur from both left and right recursion.

  1. Consider the grammar
    E → E + n | E × n | n
    For a sentence n + n × n, the handles in the right-sentential form of the reduction are








  1. View Hint View Answer Discuss in Forum

    Given grammar
    E " E + n
    E " E #n
    E " n
    String = n + n #n
    Right sentential so right most non terminal will be used.
    E " E #n {E " E #n}
    E + n #n {E " E + n}
    n + n #n {E " n}
    So during reduction the order is reverse.
    So {E " n, E " E + n, E " E #n}

    Correct Option: D

    Given grammar
    E " E + n
    E " E #n
    E " n
    String = n + n #n
    Right sentential so right most non terminal will be used.
    E " E #n {E " E #n}
    E + n #n {E " E + n}
    n + n #n {E " n}
    So during reduction the order is reverse.
    So {E " n, E " E + n, E " E #n}