A LL(1) grammar doesn't give to multiple entries in a single cell of its parsing table. It has only single entry in a single cell, hence it should be unambiguous.
Option A is wrong. Grammar is not left recursive. For a grammar to be left recursive a production should be of form A → Ab, where A is a single Non-Terminal and b is any string of grammar symbols.
Option B is wrong. Because a right recursive grammar has nothing to do with LL(1).
Option D is wrong. Because the given grammar is clearly a Context Free Grammar. A grammar is CFG if it has productions of the form A → (V ∪ T) *, where A is a single non-terminal and V is a set of Non-terminals and T is a set of Terminals.
Hence Option C should be the correct one. i.e. the grammar is ambiguous.
But let's see how the grammar is ambiguous. If the grammar is ambiguous then it should give multiple entry in a cell while making its parsing table. And Parse table is made with the aid of two functions: FIRST and FOLLOW.
A parsing table of a grammar will not have multiple entries in a cell( i.e. will be a LL(1) grammar) if and only if the following conditions hold for each production of the form A → α | β
1. FIRST (α) ∩ FIRST(β) = φ
2. If FIRST (α) contains ' ε ' then FIRST(α) ∩ FOLLOW (A) = φ and vice-versa.
Now,
• For the production, S → iCtSS1|a, rule 1 is satisfied,
because FIRST(iCtSS1) ∩ FIRST(a) = {i} ∩ {a} = φ
• For the production, S1 → eS| ε, rule 1 is satisfied,
as FIRST(eS) ∩ FIRST(ε) = {e} ∩ {e} = φ.
But here due to ' ε ' in FIRST, we have to check for rule 2. FIRST(eS) ∩ FOLLOW(S1) = {e} ∩ {e, $} ≠ φ. Hence rule 2 fails in this production rule.
Therefore there will be multiple entries in the parsing table, hence the grammar is ambiguous and not LL(1).

Correct Option: C

A LL(1) grammar doesn't give to multiple entries in a single cell of its parsing table. It has only single entry in a single cell, hence it should be unambiguous.
Option A is wrong. Grammar is not left recursive. For a grammar to be left recursive a production should be of form A → Ab, where A is a single Non-Terminal and b is any string of grammar symbols.
Option B is wrong. Because a right recursive grammar has nothing to do with LL(1).
Option D is wrong. Because the given grammar is clearly a Context Free Grammar. A grammar is CFG if it has productions of the form A → (V ∪ T) *, where A is a single non-terminal and V is a set of Non-terminals and T is a set of Terminals.
Hence Option C should be the correct one. i.e. the grammar is ambiguous.
But let's see how the grammar is ambiguous. If the grammar is ambiguous then it should give multiple entry in a cell while making its parsing table. And Parse table is made with the aid of two functions: FIRST and FOLLOW.
A parsing table of a grammar will not have multiple entries in a cell( i.e. will be a LL(1) grammar) if and only if the following conditions hold for each production of the form A → α | β
1. FIRST (α) ∩ FIRST(β) = φ
2. If FIRST (α) contains ' ε ' then FIRST(α) ∩ FOLLOW (A) = φ and vice-versa.
Now,
• For the production, S → iCtSS1|a, rule 1 is satisfied,
because FIRST(iCtSS1) ∩ FIRST(a) = {i} ∩ {a} = φ
• For the production, S1 → eS| ε, rule 1 is satisfied,
as FIRST(eS) ∩ FIRST(ε) = {e} ∩ {e} = φ.
But here due to ' ε ' in FIRST, we have to check for rule 2. FIRST(eS) ∩ FOLLOW(S1) = {e} ∩ {e, $} ≠ φ. Hence rule 2 fails in this production rule.
Therefore there will be multiple entries in the parsing table, hence the grammar is ambiguous and not LL(1).

A regular grammar can also be ambiguous also. For example, consider the following grammar,
S → aA/a
A → aA/ ε
In above grammar, string 'a' has two leftmost derivations.
(1) S → aA (2) S → a
S → a (using A → e)
And LL(1) parses only unambiguous grammar, so statement P is False.
Statement Q is true is for every regular set, we can have a regular grammar which is unambiguous so it can be parse by LR parser.
So option C is correct Answer.

Correct Option: C

A regular grammar can also be ambiguous also. For example, consider the following grammar,
S → aA/a
A → aA/ ε
In above grammar, string 'a' has two leftmost derivations.
(1) S → aA (2) S → a
S → a (using A → e)
And LL(1) parses only unambiguous grammar, so statement P is False.
Statement Q is true is for every regular set, we can have a regular grammar which is unambiguous so it can be parse by LR parser.
So option C is correct Answer.

In the language language L = {aⁱ b^j | i ≠ j} The expression i ≠ j indicates that language L is a language in which number of a ≠ number of b. Here, we need to search for a language in which number of a ≠ number of b.
Considering the options:
Options (a)
S → AC | CB
C → aCb | a| b
A → aA | ∈
B → Bb | ∈
(a), S → (C) B → a(b) → aBb → ab
Here, the number of a = number of b, hence, it is not the required grammar.
Option (b)
S → as | Sb | a | b
S → as → abB
Here, number of a = number of b, hence it is not the required grammar.
Option (c)
S → AC | CB
C → aC b| ∈
A → aA | ∈
B → Bb | ∈
S(C)B → acbB → ab
Here, number of a = number of b, hence it is not the required grammar.
Option (d)
S → AC | CB
C → aC b| ∈
A → aA | a
B → Bb | b
Consider the production
S → AC | CB
Applying, C → ∈
We get S → A|B
Now, applying A or B, S generates a^n.b^n. So, L = {aⁱ b^j | i ≠ j}
Now, consider the production, S → AC | CB. If the production C → acb is applied then, it generates a^n,b^n.
Now, applying either A or B it will give that number of a ≠ number of b.

Correct Option: D

In the language language L = {aⁱ b^j | i ≠ j} The expression i ≠ j indicates that language L is a language in which number of a ≠ number of b. Here, we need to search for a language in which number of a ≠ number of b.
Considering the options:
Options (a)
S → AC | CB
C → aCb | a| b
A → aA | ∈
B → Bb | ∈
(a), S → (C) B → a(b) → aBb → ab
Here, the number of a = number of b, hence, it is not the required grammar.
Option (b)
S → as | Sb | a | b
S → as → abB
Here, number of a = number of b, hence it is not the required grammar.
Option (c)
S → AC | CB
C → aC b| ∈
A → aA | ∈
B → Bb | ∈
S(C)B → acbB → ab
Here, number of a = number of b, hence it is not the required grammar.
Option (d)
S → AC | CB
C → aC b| ∈
A → aA | a
B → Bb | b
Consider the production
S → AC | CB
Applying, C → ∈
We get S → A|B
Now, applying A or B, S generates a^n.b^n. So, L = {aⁱ b^j | i ≠ j}
Now, consider the production, S → AC | CB. If the production C → acb is applied then, it generates a^n,b^n.
Now, applying either A or B it will give that number of a ≠ number of b.

It is very clear from the previous solution that the no. of steps required depend upon the no. of a' s & b ' s which ever is higher & exceeds by 2 due to S " AC CB & C"!
So max(l, m) + 2
Hence (a) is correct option.

Correct Option: A

It is very clear from the previous solution that the no. of steps required depend upon the no. of a' s & b ' s which ever is higher & exceeds by 2 due to S " AC CB & C"!
So max(l, m) + 2
Hence (a) is correct option.

Let's make the LR(0) set of items. First we need to augment the grammar with the production rule S' → .S, then we need to find closure of items in a set to complete a set. Below are the LR(0) sets of items.

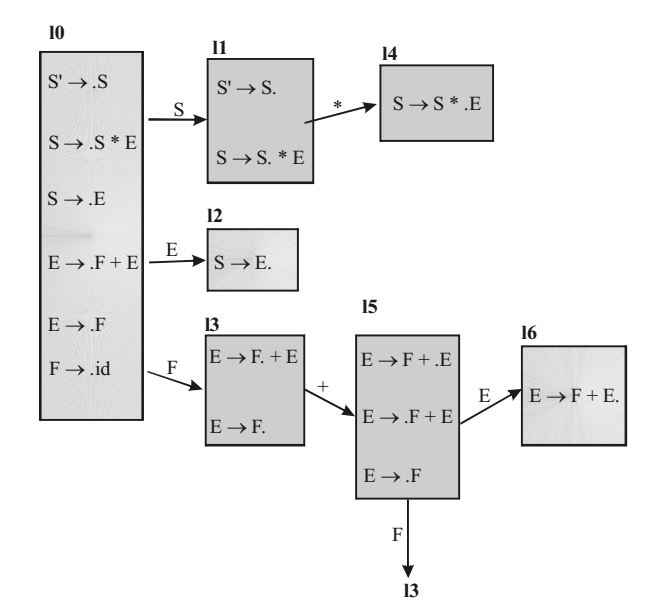
In the LR(0) sets of items formed so far, we can see that given three items belong to the different sets (13, l4, l5). Here, S' → .S is an augmented production rule.

Correct Option: D

Let's make the LR(0) set of items. First we need to augment the grammar with the production rule S' → .S, then we need to find closure of items in a set to complete a set. Below are the LR(0) sets of items.

In the LR(0) sets of items formed so far, we can see that given three items belong to the different sets (13, l4, l5). Here, S' → .S is an augmented production rule.