Thermodynamics Miscellaneous
- In the Rankine cycle for a steam power plant the turbine entry and exit enthalpies are 2803 kJ/kg and 1800 kJ/kg, respectively. The enthalpies of water at pump entry and exit are 121 kJ/kg and 124 kJ/kg respectively. The specific steam consumption (in kg/kWh) of the cycle is______.
-
View Hint View Answer Discuss in Forum
Pump work
Wp = h2 – h1 = 124 – 121 = 3kJ/kg
Power output
wt = hu – hs = 2803 – 1800 = 1003 kJ/kg
Net output Wnet = wt – wp = 1003 – 3 = 1000 k
Specific steam consumption= 3600 (kg / kW - h) = 3.6 kg/kW – h Wnet
Correct Option: A
Pump work
Wp = h2 – h1 = 124 – 121 = 3kJ/kg
Power output
wt = hu – hs = 2803 – 1800 = 1003 kJ/kg
Net output Wnet = wt – wp = 1003 – 3 = 1000 k
Specific steam consumption= 3600 (kg / kW - h) = 3.6 kg/kW – h Wnet
- The pressure ratio across a gas turbine (for air, specific heat at constant pressure, cp = 1040 J/ kg K and ratio of specific heats η = 1.4) is 10. If the inlet temperature to the turbine is 1200 K and the isentropic efficiency is 0.9, the gas temperature at turbine exit is ________K.
-
View Hint View Answer Discuss in Forum

By question
T1 = 1200 Krp = 10 = P1 P1
ηT = 0.9
T2 =?
T2 = 621.53 KηT = T1 - T2 T1 - T2 0.9 = 1200 - T2 1200 - 621.53
T2 = 679.4 K
Correct Option: A

By question
T1 = 1200 Krp = 10 = P1 P1
ηT = 0.9
T2 =?
T2 = 621.53 KηT = T1 - T2 T1 - T2 0.9 = 1200 - T2 1200 - 621.53
T2 = 679.4 K
- In a steam power plant operating on a ideal Rankine cycle, superheated steam enters the turbine at 3 MPa and 350°C. The condenser pressure is 75 kPa. The thermal efficiency of the cycle is ________%. Given data: For saturated liquid, at p = 75 kPa, hf = 384.39 kJ/kg, vf = 0.001037 m3/kg, sf = 1.213 kJ/kgK. At 75 kPa, hfg = 2278.6 kJ/kg, sfg = 6.2434 kJ/kgK At P = 3 MPa and T = 350°C (superheated steam), h = 3115.3 kJ/kg, s = 6.7428 kJ/kgK.
-
View Hint View Answer Discuss in Forum

h1 = 3115.3 kJ/kg
s1 = 6.7428 kJ/kg
s1 = s2 = sf + xsfgx = 6.7428 - 1.213 = 5.5298 = 0.8857 6.2434 6.2434
h2 = hf + xhfg
= 348.39 + 0.8857 × 2278.6
= 348.39 + 2018.16
= 2402.55 kJ/kg
Pump work = Wp = vf (p4 – p3) = 3.033 kJ/kg
h4 = h3 + vf (p4 – p3)
= 384.34 + 0.001037(3000 – 75)
= 384.34 + 3.033 = 387.37 kJ/kg
Wnet = WT – WP = (h1 – h2) – WP
= (3115.3 – 2402.55) – 3.033
= 709.72 kJ/kg
Qs = heat supplied = h1 – h4
= 3115.3 – 387.37
= 2727.93 kJ/kgηth = Wnet Qs = 709.72 × 100 = 0.26 or 26% 2727.93
Correct Option: A

h1 = 3115.3 kJ/kg
s1 = 6.7428 kJ/kg
s1 = s2 = sf + xsfgx = 6.7428 - 1.213 = 5.5298 = 0.8857 6.2434 6.2434
h2 = hf + xhfg
= 348.39 + 0.8857 × 2278.6
= 348.39 + 2018.16
= 2402.55 kJ/kg
Pump work = Wp = vf (p4 – p3) = 3.033 kJ/kg
h4 = h3 + vf (p4 – p3)
= 384.34 + 0.001037(3000 – 75)
= 384.34 + 3.033 = 387.37 kJ/kg
Wnet = WT – WP = (h1 – h2) – WP
= (3115.3 – 2402.55) – 3.033
= 709.72 kJ/kg
Qs = heat supplied = h1 – h4
= 3115.3 – 387.37
= 2727.93 kJ/kgηth = Wnet Qs = 709.72 × 100 = 0.26 or 26% 2727.93
- Steam at a velocity of 10 m/s enters the impulse turbine stage with symmetrical blading having blade angle 30°. The enthalpy drop in the stage is 100 kJ. The nozzle angle is 20°. The maximum blade efficiency (in percent) is ____.
-
View Hint View Answer Discuss in Forum
85.1 to 89.9
Maximum blade efficiency
η max = cos² α
= .883
= 88.3%Correct Option: A
85.1 to 89.9
Maximum blade efficiency
η max = cos² α
= .883
= 88.3%
- Specific enthalpy and velocity of steam at inlet and exit of a steam turbine, running under steady state, are as given below:

The rate of heat loss from the turbine per kg of steam flow rate is 5 kW. Neglecting changes in potential energy of steam, the power developed in kW by the steam turbine per kg of steam flow rate, is
-
View Hint View Answer Discuss in Forum
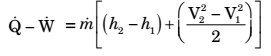
and Q = – 5 kW, m = 1 kg / sCorrect Option: A
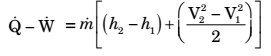
and Q = – 5 kW, m = 1 kg / s

