Programming and data structure miscellaneous
- Which combination of the integer variables x, y and z makes the variable a get the value 4 in the following expression ?
a = (x > y)? ((x > z)? x : z) : ((y > z)? y : z)
-
View Hint View Answer Discuss in Forum
The operator “?:” in C is the ternary operator which means that, if the expression is exp 1? exp2: exp3, so it means, if exp1 is true then exp2 is returned as the answer else exp3 is the required answer.
So, in the given expression let us consider x = 3, y = 4, z = 2,
Then, expression becomes a = (3 > 4)? ((3 > 2)? 3:2): ((4>2?4:2)
From this, we get that 3>4 is false so we go for the else part of the statement which is 4>2 and is true thus, the answer is 4, the true part of the statement.Correct Option: A
The operator “?:” in C is the ternary operator which means that, if the expression is exp 1? exp2: exp3, so it means, if exp1 is true then exp2 is returned as the answer else exp3 is the required answer.
So, in the given expression let us consider x = 3, y = 4, z = 2,
Then, expression becomes a = (3 > 4)? ((3 > 2)? 3:2): ((4>2?4:2)
From this, we get that 3>4 is false so we go for the else part of the statement which is 4>2 and is true thus, the answer is 4, the true part of the statement.
- Consider the program below :
#include < stdio.h >
int fun (int n, int * f_p){
int t, f;
if (n < = 1) {
*f_p = 1
return 1;
}
t = fun (n – 1, *f_p);
f = t + *f_p; *f_p = t;
return f;
}
int main () {
int x = 15;
printf (“% d\n”, fun (5, & x));
return 0;
}
The value printed is
-
View Hint View Answer Discuss in Forum
The program calculates nth Fibonacci Number. The statement t = fun (n-1, fp) gives the (n-1)th Fibonacci number and *fp is used to store the (n-2)th Fibonacci Number. Initial value of *fp (which is 15 in the above program) doesn't matter. Following recursion tree shows all steps from 1 to 10, for exceution of fun(5, &x).
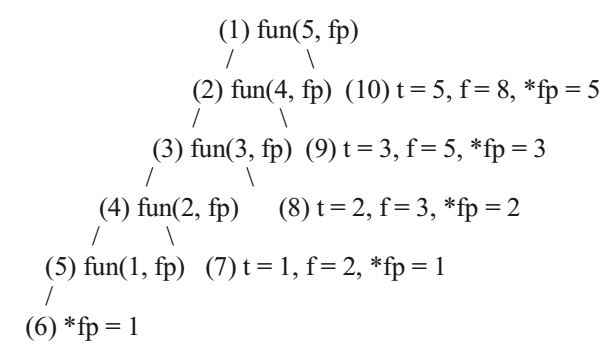
Correct Option: B
The program calculates nth Fibonacci Number. The statement t = fun (n-1, fp) gives the (n-1)th Fibonacci number and *fp is used to store the (n-2)th Fibonacci Number. Initial value of *fp (which is 15 in the above program) doesn't matter. Following recursion tree shows all steps from 1 to 10, for exceution of fun(5, &x).
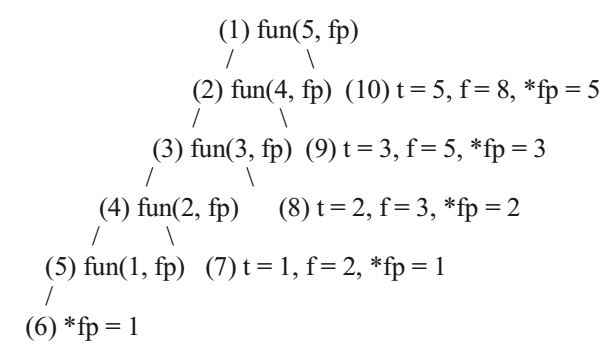
- What is the value printed by the following C program ?
#include < stdio.h>
int f (int *a, int n)
{
if (n < = 0) return 0;
else if (*a% 2 = = 0) return *a + f(a + 1, n – 1);
else return *a – f(a + 1, n – 1);
}
int main ()
{
int a [] = {12, 7, 13, 4, 11, 6};
print f (“%d, f(a, 6));
return 0,
}
-
View Hint View Answer Discuss in Forum
f() is a recursive function which adds f(a + 1, n – 1) to *a if *a is even. If *a is odd then f() subtracts f(a + 1, n – 1) from *a. See below recursion tree for execution of f(a, 6).
f(add(12), 6) /*Since 12 is first element. a contains
address of 12 */
|
|
12 + f(add(7), 5) /* Since 7 is the next element, a+1 contains address of 7 */
|
|
7 – f(add(13), 4)
|
|
13 – f(add(4), 3)
|
|
4 + f(add(11), 2)
|
|
11 – f(add(6), 1)
|
|
6 + 0
So, the final returned value is
12 + (7 – (13 – (4 + (11 – (6 + 0))))) = 15Correct Option: C
f() is a recursive function which adds f(a + 1, n – 1) to *a if *a is even. If *a is odd then f() subtracts f(a + 1, n – 1) from *a. See below recursion tree for execution of f(a, 6).
f(add(12), 6) /*Since 12 is first element. a contains
address of 12 */
|
|
12 + f(add(7), 5) /* Since 7 is the next element, a+1 contains address of 7 */
|
|
7 – f(add(13), 4)
|
|
13 – f(add(4), 3)
|
|
4 + f(add(11), 2)
|
|
11 – f(add(6), 1)
|
|
6 + 0
So, the final returned value is
12 + (7 – (13 – (4 + (11 – (6 + 0))))) = 15
- The program below uses six temporary variables a, b, c, d, e, f.
a = 1
b = 10
c = 20
d = a + b
e = c + d
f = c + e
b = c + e
e = b + f
d = 5 + e
return d + f Assuming that all operations take their operands from registers, what is the minimum number of registers needed to execute this program without spilling ?
-
View Hint View Answer Discuss in Forum
Let AX, BX, CX be three registers used to store results of temporary variables a, b, c, d, e, f.
a(AX) = 1
b(BX) = 10
c(CX) = 20
d(AX) = a(AX) + b(BX)
e(BX) = c(CX) + d(AX)
f(AX) = c(CX) + e(BX)
b(BX) = c(CX) + e(BX)
e(BX) = b(BX) + f(AX)
d(CX) = 5 + e(BX)
return d(CX) + f(AX)
Thus, only 3 registers can be used without any overwriting of data.Correct Option: B
Let AX, BX, CX be three registers used to store results of temporary variables a, b, c, d, e, f.
a(AX) = 1
b(BX) = 10
c(CX) = 20
d(AX) = a(AX) + b(BX)
e(BX) = c(CX) + d(AX)
f(AX) = c(CX) + e(BX)
b(BX) = c(CX) + e(BX)
e(BX) = b(BX) + f(AX)
d(CX) = 5 + e(BX)
return d(CX) + f(AX)
Thus, only 3 registers can be used without any overwriting of data.
- The following program is to be tested for statement coverage.
begin
if (a = = b) {S1; exit;}
else, if (c = = d) {S2;}
else {S3; exit;}
S4;
end
The test cases T1, T2, T3 and T4 given below are expressed in terms of the properties satisfied by the values of variables a, b, c and d. The exact values are not given.
T1 : a, b, c and d are all equal
T2 : a, b, c and d are all distinct
T3 : a = b and c! = d
T4 : a! = b and c = d
Which of the test suites given below ensures coverage of statements S1, S12, S3 and S4 ?
-
View Hint View Answer Discuss in Forum
In a given program we take the test cases and apply.
First take T1, if all value equal means
a = b = c = d
So, due to T1, a = b condition satisfied and S1 and S4 executed.
So, from T2 when all a, b, c, d distinct.
S1, S2 not execute, S3 execute.
from T3 when a = b then, S1 execute but c = d so, S2 not execute but S3 and S4 execute but we have no need of T3 because we get all result from above two.
By using T4. If a! = b and c = d
So, S1 not execute and S2 and S4 execute so all of S1, S2, S3, S4 execute and covered by T1, T2 and T4.Correct Option: D
In a given program we take the test cases and apply.
First take T1, if all value equal means
a = b = c = d
So, due to T1, a = b condition satisfied and S1 and S4 executed.
So, from T2 when all a, b, c, d distinct.
S1, S2 not execute, S3 execute.
from T3 when a = b then, S1 execute but c = d so, S2 not execute but S3 and S4 execute but we have no need of T3 because we get all result from above two.
By using T4. If a! = b and c = d
So, S1 not execute and S2 and S4 execute so all of S1, S2, S3, S4 execute and covered by T1, T2 and T4.

