Programming and data structure miscellaneous

Programming and data structure miscellaneous

Easy Questions

Programming & Data Structure

Programming and data structure miscellaneous
  1. In a complete k-array tree, every internal node has exactly k children. The number of leaves in such a tree with n internal nodes is








  1. View Hint View Answer Discuss in Forum

    No. of internal nodes = n Each node has k children
    So total nk
    Leaf nodes = nk – n
    = n(k – 1)
    So considering not node also.
    No. of leaf nodes = n(k – 1) + 1
    Hence (c) is correct option.

    Correct Option: C

    No. of internal nodes = n Each node has k children
    So total nk
    Leaf nodes = nk – n
    = n(k – 1)
    So considering not node also.
    No. of leaf nodes = n(k – 1) + 1
    Hence (c) is correct option.

  1. A complete n-array tree is a tree in which each node has n children or no children. Let l be the number of internal nodes and L be the number of leaves in a complete n-array tree. If L = 41, and l = 10, what is the value of n?








  1. View Hint View Answer Discuss in Forum

    Each internal node has n children & so total nodes n No. of leaf in them is :
    ⇒ I* (n – 1)
    ⇒ I(n – 1)
    But root can’t produce leaf
    I(n – 1) + 1 = L
    n = L – 1 / l + 1
    n = (41 – 1 )/10 + 1 = 5

    Correct Option: C

    Each internal node has n children & so total nodes n No. of leaf in them is :
    ⇒ I* (n – 1)
    ⇒ I(n – 1)
    But root can’t produce leaf
    I(n – 1) + 1 = L
    n = L – 1 / l + 1
    n = (41 – 1 )/10 + 1 = 5

  1. A B-tree of order 4 is built from scratch by 10 successive insertions. What is the maximum number of node splitting operations that may take place?








  1. View Hint View Answer Discuss in Forum

    Let’s take 10 successive key value {1, 2, 3..........10}


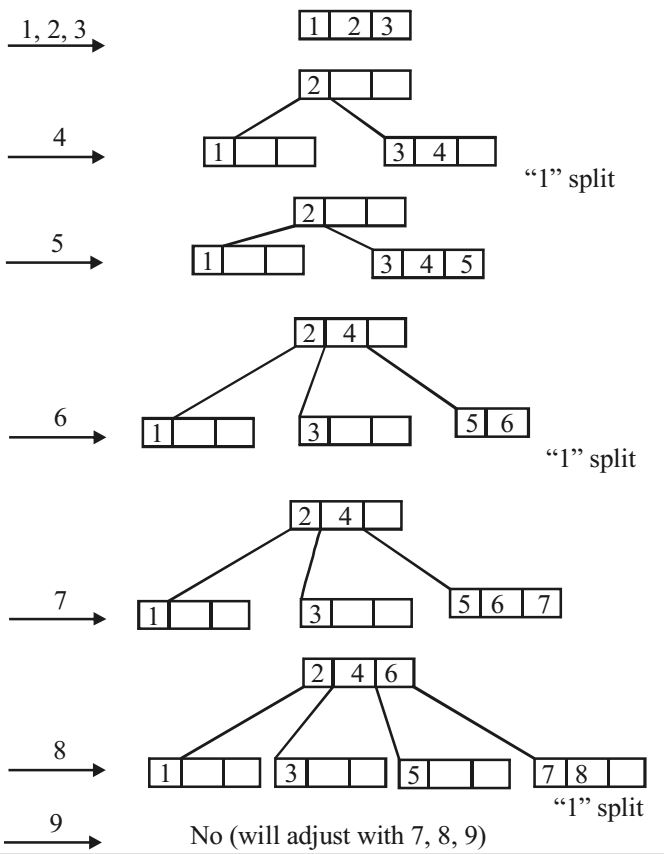
    Correct Option: C

    Let’s take 10 successive key value {1, 2, 3..........10}


  1. What is the maximum height of any AVL-tree with 7 nodes? Assume that the height of a tree with a single node is 0.








  1. View Hint View Answer Discuss in Forum

    AVL trees are binary trees with the following restrictions.
    (1) the height difference of the children is at most 1.
    (2) both children are AVL trees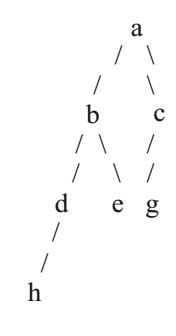

    Correct Option: B

    AVL trees are binary trees with the following restrictions.
    (1) the height difference of the children is at most 1.
    (2) both children are AVL trees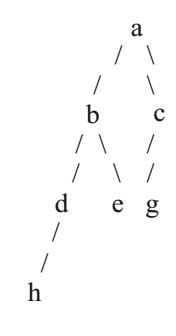

  1. Consider evaluating the following expression tree on a machine with load store architecture in which memory can be accessed only through load and store instructions. The variables a, b, c, d and e are initially stored in memory. The binary operators used in this expression tree can be evaluated by the machine only when the operands are in registers. The instructions produce result only in a register. If no intermediate results can be stored in memory, what is the minimum number of registers needed to evaluate this expression?









  1. View Hint View Answer Discuss in Forum

    R1 ← c, R2 ← d, R2 ← R1 + R2, R1 ← e, R2 ← R1-R2 Now to calculate the rest of the expression we must load a and b into the registers but we need the content of R2 later. So we must use another Register. R1 ← a, R3 ← b, R1 ← R1-R3, R1 ← R1 + R2

    Correct Option: D

    R1 ← c, R2 ← d, R2 ← R1 + R2, R1 ← e, R2 ← R1-R2 Now to calculate the rest of the expression we must load a and b into the registers but we need the content of R2 later. So we must use another Register. R1 ← a, R3 ← b, R1 ← R1-R3, R1 ← R1 + R2