Programming and data structure miscellaneous

Programming and data structure miscellaneous

Easy Questions

Programming & Data Structure

Programming and data structure miscellaneous
  1. The number of ways in which the numbers 1, 2, 3, 4, 5, 6, 7 can be inserted in an empty binary search tree, such that the resulting tree has height 6, is ________.
    Note : The height of a tree with a single node is 0.








  1. View Hint View Answer Discuss in Forum

    To fill 7 levels with 7 elements, at each level we have exactly 2 possible options like 1 and 7 for root one corresponding to making it left skewed and other right skewed. This is valid for all levels upto 6.
    Hence, 26 = 64.

    Correct Option: D

    To fill 7 levels with 7 elements, at each level we have exactly 2 possible options like 1 and 7 for root one corresponding to making it left skewed and other right skewed. This is valid for all levels upto 6.
    Hence, 26 = 64.

  1. Consider the following New-order strategy for traversing a binary tree :
    • Visit the root;
    • Visit the right subtree using New-order;
    • Visit the left subtree using New-order;
    The New-order traversal of the expression tree corresponding to the reverse polish expression 3 4 * 5 – 2 ^ 6 7 * 1 + – is given by :








  1. View Hint View Answer Discuss in Forum

    The expression tree for the given post-fix expression is as follows :

    New-order of shown expression tree is – + 1 * 7 6 ^ 2 – 5 * 4 3

    Correct Option: C

    The expression tree for the given post-fix expression is as follows :

    New-order of shown expression tree is – + 1 * 7 6 ^ 2 – 5 * 4 3

  1. B+ Trees are considered BALANCED because








  1. View Hint View Answer Discuss in Forum

    In B and B+ trees, all the leaf nodes will be at same level.

    Correct Option: A

    In B and B+ trees, all the leaf nodes will be at same level.

  1. In a B+ tree, if the search-key value is 8 bytes long, the block size is 512 bytes and the block pointer size is 2 bytes, then the maximum order of the B+ tree is ______.








  1. View Hint View Answer Discuss in Forum

    As given that: Search key = 8 bytes Block size = 512 bytes. Block pointer (BP) = 2 bytes. Then maximum order of B+ tree is Let K is the order then, K * Bp + (K - 1)*Key ≤ Block size
    K *2 + (K - 1)*8 ≤ 512
    10K ≤ (512 + 8)
    10K ≤ 520

    K =
    520
    		 = 52
    10

    Hence, 52 is correct answer.

    Correct Option: B

    As given that: Search key = 8 bytes Block size = 512 bytes. Block pointer (BP) = 2 bytes. Then maximum order of B+ tree is Let K is the order then, K * Bp + (K - 1)*Key ≤ Block size
    K *2 + (K - 1)*8 ≤ 512
    10K ≤ (512 + 8)
    10K ≤ 520

    K =
    520
    		 = 52
    10

    Hence, 52 is correct answer.

  1. The pre-order traversal of a binary search tree is given by 12, 8, 6, 2, 7, 9, 10, 16, 15, 19, 17, 20. Then the postorder traversal of this tree is :








  1. View Hint View Answer Discuss in Forum

    For the given pre-order traversal of a binary search tree, Pre order is : (Root, left, Right)
    Pre order : 12, 8, 6, 2, 7, 9, 10, 16, 15, 19, 17, 20
    In order is : (Left, Root, Right),
    So in order of given sequence is : 2, 6, 7, 8, 9, 10, 12, 15, 16, 17, 19, 20.
    Then tree will be :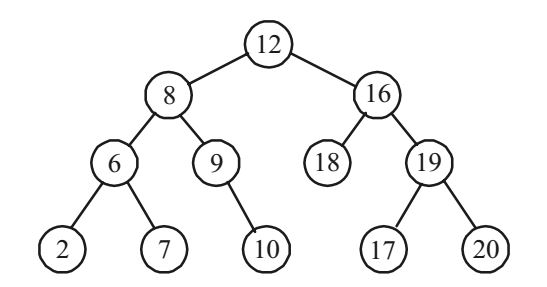

    Now, post order is : (Left, Right, Root)
    Post order will be, 2, 7, 6, 10, 9, 8, 15, 17, 20, 19, 16, 12
    Hence option (b) is correct.

    Correct Option: B

    For the given pre-order traversal of a binary search tree, Pre order is : (Root, left, Right)
    Pre order : 12, 8, 6, 2, 7, 9, 10, 16, 15, 19, 17, 20
    In order is : (Left, Root, Right),
    So in order of given sequence is : 2, 6, 7, 8, 9, 10, 12, 15, 16, 17, 19, 20.
    Then tree will be :

    Now, post order is : (Left, Right, Root)
    Post order will be, 2, 7, 6, 10, 9, 8, 15, 17, 20, 19, 16, 12
    Hence option (b) is correct.