Motion in a Straight Line
- A car moving with a speed of 40 km/h can be stopped by applying brakes at least after 2 m. If the same car is moving with a speed of 80 km/h, what is the minimum stopping distance?
-
View Hint View Answer Discuss in Forum
v² – u² = 2as
⇒ a = v² - u² 2s = - u1² , where u1 = 40 km/h 2s
For same retarding force s ∝ u²∵ s2 = u2² ⇒ s2 = 
80 
² = 4 s1 u1² s1 40
∴ s2 = 4s1 = 8m
If F is retarding force and s the stopping distance, then 1/2 mv² = Fs
For same retarding force, s α v²∴ s2 = 
v2 
² = 
80 km/h 
² = 4 s1 v1 40 km/h
∴ s2 = 4s1 = 4 × 2 = 8mCorrect Option: A
v² – u² = 2as
⇒ a = v² - u² 2s = - u1² , where u1 = 40 km/h 2s
For same retarding force s ∝ u²∵ s2 = u2² ⇒ s2 = 
80 
² = 4 s1 u1² s1 40
∴ s2 = 4s1 = 8m
If F is retarding force and s the stopping distance, then 1/2 mv² = Fs
For same retarding force, s α v²∴ s2 = 
v2 
² = 
80 km/h 
² = 4 s1 v1 40 km/h
∴ s2 = 4s1 = 4 × 2 = 8m
- The displacement of a particle varies withtime (t) as: s = at² – bt³. The acceleration of the particle at any given time (t) will be equal to
-
View Hint View Answer Discuss in Forum
s = at² – bt³
v = ds = 2at - 3bt² dt a = dv = 2a - 6bt dt
2a - 6bt = 0⇒ a 3b Correct Option: B
s = at² – bt³
v = ds = 2at - 3bt² dt a = dv = 2a - 6bt dt
2a - 6bt = 0⇒ a 3b
- A car accelerates from rest at a constant rate α for some time, after which it decelerates at a constant rate β and comes to rest. If the total time elapsed is t, then the maximum velocity acquired by the car is
-
View Hint View Answer Discuss in Forum
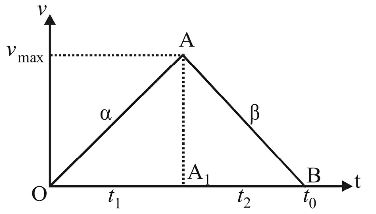
In Fig.
AA1 = vmax. = αt1 = βt2
But t = t1 + t2 = vmax./α + vmax./β= vmax. 
1 + 1 
= vmax. 
α + β 
α β αβ or, = vmax. = t 
αβ 
α + β Correct Option: D

In Fig.
AA1 = vmax. = αt1 = βt2
But t = t1 + t2 = vmax./α + vmax./β= vmax. 
1 + 1 
= vmax. 
α + β 
α β αβ or, = vmax. = t 
αβ 
α + β
- The water drops fall at regular intervals from a tap 5 m above the ground. The third drop is leaving the tap at an instant when the first drop touches the ground. How far above the ground is the second drop at that instant ? (Take g = 10 m/s²)
-
View Hint View Answer Discuss in Forum
Height of tap = 5m and (g) = 10 m/sec².
For the first drop, 5 = ut + (1/2) gt²
= (0 × t) + (1/2) = 5t² or t² = 1 or t = 1 sec.
It means that the third drop leaves after one second of the first drop. Or, each drop leaves after every 0.5 sec.
Distance covered by the second drop in 0.5 sec= ut + 1 gt² = (0 × 0.5) + 1 × 10 × (0.5)² 2 2
= 1.25 m.
Therefore, distance of the second drop above the ground = 5 – 1.25 = 3.75 m.Correct Option: C
Height of tap = 5m and (g) = 10 m/sec².
For the first drop, 5 = ut + (1/2) gt²
= (0 × t) + (1/2) = 5t² or t² = 1 or t = 1 sec.
It means that the third drop leaves after one second of the first drop. Or, each drop leaves after every 0.5 sec.
Distance covered by the second drop in 0.5 sec= ut + 1 gt² = (0 × 0.5) + 1 × 10 × (0.5)² 2 2
= 1.25 m.
Therefore, distance of the second drop above the ground = 5 – 1.25 = 3.75 m.
- The displacement time graph of a moving particle is shown below
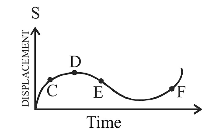
The instantaneous velocity of the particle is negative at the point
-
View Hint View Answer Discuss in Forum
At E, the slope of the curve is negative.
Correct Option: D
At E, the slope of the curve is negative.

