Motion in a Straight Line
- A particle has initial velocity (3î + 4ĵ) and has acceleration (0.4 î + 0.3 ĵ). It's speed after 10 s is:
-
View Hint View Answer Discuss in Forum
→u = 3î + 4ĵ,→a = 0.4î + 0.3ĵ
⇒ ux = 3 units, uy = 4 units
ax = 0.4 units, ay = 0.3 units
∴ vx + ax × 10 = 3 + 4 = 7 ms–1
and vy = 4 + 0.3 × 10 = 4 + 3 = 7 ms–1
∴ v = √vx² + vy²
= 7√2 ms–1Correct Option: B
→u = 3î + 4ĵ,→a = 0.4î + 0.3ĵ
⇒ ux = 3 units, uy = 4 units
ax = 0.4 units, ay = 0.3 units
∴ vx + ax × 10 = 3 + 4 = 7 ms–1
and vy = 4 + 0.3 × 10 = 4 + 3 = 7 ms–1
∴ v = √vx² + vy²
= 7√2 ms–1
- A particle has initial velocity (2
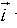+ 3
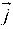) and acceleration (0.3 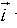+ 0.2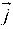). The magnitude of velocity after 10 seconds will be :
-
View Hint View Answer Discuss in Forum
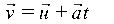
= v = (2î + 3ĵ) + (0.3î + 0.2ĵ) × 10 = 5î + 5ĵ
|v| = √5² + 5 ²
|v| = 5 √2Correct Option: D
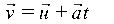
= v = (2î + 3ĵ) + (0.3î + 0.2ĵ) × 10 = 5î + 5ĵ
|v| = √5² + 5 ²
|v| = 5 √2
- The motion of a particle along a straight line is described by equation :
x = 8 + 12t – t³
where x is in metre and t in second. The retardation of the particle when its velocity becomes zero, is :
-
View Hint View Answer Discuss in Forum
x = 8 + 12t – t³
The final velocity of the particle will be zero, because it retarded.
V = 0 + 12 – 3t² = 0
3t² = 12
t = 2 sec
Now the retardation
a = dv/dt = 0 – 6t
a [t = 2] = – 12 m/s²
retardation = 12 m/s²Correct Option: D
x = 8 + 12t – t³
The final velocity of the particle will be zero, because it retarded.
V = 0 + 12 – 3t² = 0
3t² = 12
t = 2 sec
Now the retardation
a = dv/dt = 0 – 6t
a [t = 2] = – 12 m/s²
retardation = 12 m/s²
- The displacement ‘x’ (in meter) of a particle of mass ‘m’ (in kg) moving in one dimension under the action of a force, is related to time ‘t’ (in sec) by t = √x + 3. The displacement of the particle when its velocity is zero, will be
-
View Hint View Answer Discuss in Forum
∵ t = √x - 3
⇒ √x = t – 3 ⇒ x = (t – 3)²
v = dx/dt = 2(t – 3) = 0
⇒ t = 3
∴ x = (3 – 3)²
⇒ x = 0.Correct Option: C
∵ t = √x - 3
⇒ √x = t – 3 ⇒ x = (t – 3)²
v = dx/dt = 2(t – 3) = 0
⇒ t = 3
∴ x = (3 – 3)²
⇒ x = 0.
- A particle starts its motion from rest under the action of a constant force. If the distance covered in first 10 seconds is S1 and that covered in the first 20 seconds is S2, then:
-
View Hint View Answer Discuss in Forum
u = 0, t1 = 10s, t2 = 20s
Using the relation, S = ut + 1/2 at²
Acceleration being the same in two cases,
S1 = (1/2)a × t1², S2 = (1/2)a × t2²
∴ S1/S2 = (t1/t2)² = (10/20)² = 1/4
S2 = 4S1Correct Option: B
u = 0, t1 = 10s, t2 = 20s
Using the relation, S = ut + 1/2 at²
Acceleration being the same in two cases,
S1 = (1/2)a × t1², S2 = (1/2)a × t2²
∴ S1/S2 = (t1/t2)² = (10/20)² = 1/4
S2 = 4S1
