The signum function is given by sgn(x) = x/|x|, x≠00 x

The signum function is given by
sgn(x) = x/|x|, x≠0
0 x = 0

The fourier series expansion of sgn(cos(t)) has

1. only sine terms with all harmonics
2. only cosine terms with all harmonics
3. only sine terms with even numbered harmonics
4. only cosine terms with odd numbered harmonics

The signum function is given by,

sgn(x) =		x/\|x\|;		x ≠ 0
sgn(x) =		0;		x = 0

Similarly,

sgn(cos t) =		cos/\|cos t\|;		cos t ≠ 0
sgn(cos t) =		- 1;		cos t = 0

cos t / \|cos t\| =		1,		cos t > 0
cos t / \|cos t\| =		- 1;		cos t < 0

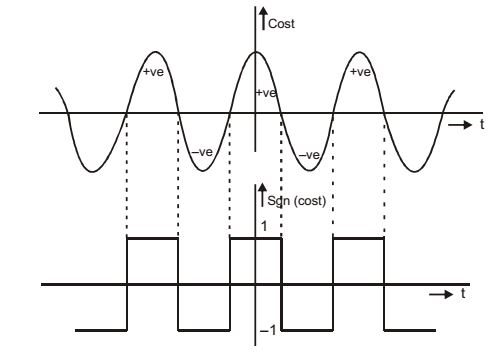
It is even function and show half wave symmetry. It contains only cosine term with odd numbered harmonics. a₀ = 0
b_n = 0

a_n =		0;		n = even
a_n =		≠0;		n = odd

Sgn(Cost) = a₁ cosωt + a₃ cos3ωt + a₅cos5ωt +...