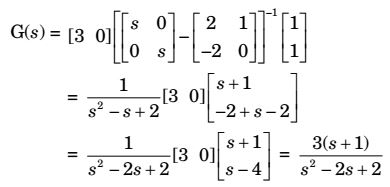For the system governed by the set of equations: dx1/dt

For the system governed by the set of equations:
dx₁/dt = 2x₁ + x₂ + 4
dx₂ /dt = – 2x₁ + 4
y = 3x₁
the transfer function Y(s)/U(s) is given by

1. 3(s + 1)/(s² – 2s + 2)
2. 3(2s + 1)(s² – 2s + 1)
3. (s + 1)/(s² – 2s + 1)
4. 3(2s + 1)(s² – 2s + 2)

dx₁	= 2x₁ + x₂ + 4
dt

dx₂	= - 2x₁ + 4
dt

y = 3x₁
Now from the standard equation x_i = Ax + BU
y = Cx + DU

	x₁		=		2	1			x₁		+		1		[4]
	x₂				- 2	2			x₂				1

y = [3 0]		x₁
		x₂

Transfer function	y(s)	C(SI - A)^-1 B
	u(s)