Direction: The figure (not drawn on scale) given below shows the aerial distance (in km) between 8 cities, e.g. distance between H and F is 600 km etc.
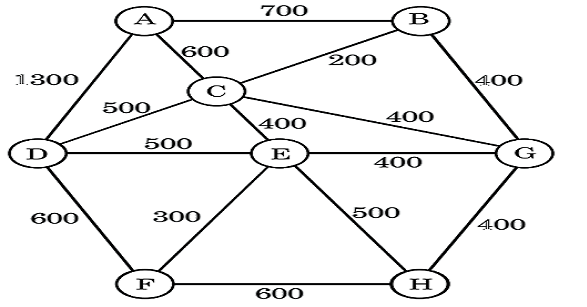
-
Find the total number of paths from city H to city A if condition is that traveling a city more than once is not allowed.
-
- 44
- 55
- 59
- None of these
Correct Option: B
Number of paths is as follows:
Starting from HGB: HGBA, HGBCA, HGBCDA, HGBCEDA, HGBCEFDA (Total 5 paths)
Starting from HGC: HGCA, HGCBA, HGCDA, HGCEDA, HGCEFDA (Total 5 paths)
Starting from HGE: HGECA, HGECBA, HGECDA, HGEDCA, HGEDCBA, HGEDA, HGEFDCBA, HGEFDCA, HGEFDA (Total 9 paths)
Starting from HEG: HEGBA, HEGCBA, HEGCA, HEGCDA (Total 4 paths)
Starting from HEC: HECGBA, HECBA, HECA, HECDA (Total 4 paths) Starting from HED: HEDCBGA, HEDCBA, HEDCA, HEDA (Total 4 paths)
Starting from HEF: HEFDCGBA, HEFDCBA, HEFDCBA, HEFDCA, HEFDA (Total 5 paths)
Starting from HFE: HFEGBA, HFECGBA, HFECBA, HFECA, HFEDCGBA, HFEDCBA, HFEDCA, HFEDA, (Total 8 paths)
Starting from HFD: HFDEGBA, HFDEGCA, HFDEGBCA, HFDECGBA, HFDECBA, HFDECA, HFDCEBGA, HFDCGBA, HFDCBA, HFDCA, HFDA (Total 11 paths)
Total number of paths is: 5 + 5 + 9 + 4 + 4 + 4 + 5 + 8 + 11 = 55
Hence , the total number of paths from city H to city A is 55 .

