Direction: There are 5 cities A, B, C, D and E connected by 7 roads as shown in the figure below :
Design a route such that you start from any city of your choice and walk on each of the 7 roads once and only once, not necessarily returning to the city from which you started.
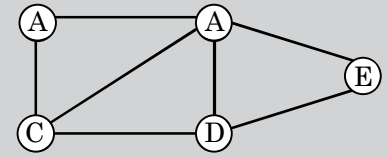
-
How many different starting cities are possible such that the above restriction is satisfied?
-
- One
- Zero
- Three
- Two
Correct Option: D
On the basis of above given figure , we can see that
City A is connected by 2 roads, B by 4 roads, C by 3 roads, D by 3 roads and E by 2 roads.
For a city to be starting city for such a route, it has to be connected by odd number of roads.
Hence the required answer is 2, i.e. C and D.

