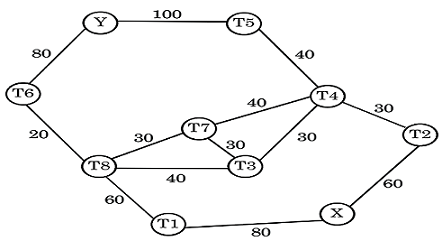
Direction: A city has hexagonal ring road as shown in the figure below. Mr. Ricky stays at X near city and his office is located at Y. The arrow in the figure shows flow of traffic at office hours. The numerical value near each path shows the cost of travel along that road/stretch of the road. There is a fix toll tax at each of toll booths T1, T2...............… T8. The total cost of travel includes cost incurred along the path and at the toll booth.
-
If toll tax at all of the toll booths is same and is devised such that the ratio of maximum cost to minimum cost of travel from X to Y is 28 : 19 then which one of the following is the cost of travel from X to Y through toll Both T3?
-
- 320 or 510
- 330 or 560
- 560 or 510
- None of these
Correct Option: C
If toll tax at all of the toll booths is same and let it be k then expense in each path is as follows:
Path 1: 240 + 3k
Path 2: 260 + 5k
Path 3: 260 + 6k
Path 4: 260 + 5k
Path 5: 230 + 3k
So from the given condition On solving we will get k = 50
Tool booth 3 will come in Path 3 and Path 4.
So cost incurred is:
Path 3: 260 + 6k = 260 + 300 = 560
Path 4: 260 + 5k = 260 + 250 = 510
Therefore , 560 or 510 is the cost of travel from X to Y through toll Both T3 .

