Concrete structures miscellaneous
Direction: 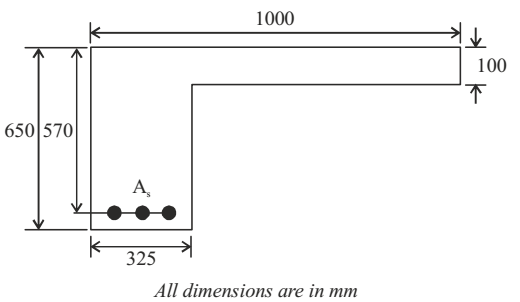
The cross-section at mid-span of a beam at the edge of a slab is shown in the sketch. A portion of the slab is considered as the effective flange width for the beam. The grades of concrete and reinforcing steel are M25 and Fe415, respectively. The total area of reinforcing bars (As) is 4000 mm2. At the ultimate limit state, xu denotes the depth of the neutral axis from the top fibre. Treat the section as under-reinforced and flanged (xu > 100 mm).
- The ultimate moment capacity (in kNm) of the section, as per the Limit State Method of IS 456: 2000 is
-
View Hint View Answer Discuss in Forum
mu = muw + muf
= [0.36 fch bw. xu (d – 0.416 xu)] +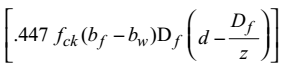
= 720.08 kNmCorrect Option: B
mu = muw + muf
= [0.36 fch bw. xu (d – 0.416 xu)] +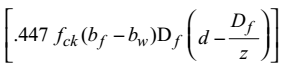
= 720.08 kNm
Direction: A reinforced concrete beam of rectangular cross section of breadth 230 mm and effective depth 400 mm is subjected to a maximum factored shear force of 120 kN. The grade of concrete, mains steel and stirrup steel are M20, F415 and Fe250 respectively. For the area of main steel provided, the design shear strength τc as per IS : 456-2000 is 0.48 N/mm2. The beam is designed for collapse limit state.
- The spacing (mm) of 2-legged 8 mm stirrups to be provided is
-
View Hint View Answer Discuss in Forum
Total shear force = 0.48 × 230 × 400 =
44.16 kN (< 120kN)
∴ Net shear force, Vus = 120 – 44.16 = 75.84 kN
If ‘s’ is the spacing of sheer reinforcementVs = d × 0.87 × fy × Ast xs Ast = 2 × π × 82 = 100.53 mm2 4 ∴ s = d × 0.87 fy Ast Vus = 400 × 0.87 × 250 × 100.53 = 115.323 mm 75.84 × 103 Correct Option: B
Total shear force = 0.48 × 230 × 400 =
44.16 kN (< 120kN)
∴ Net shear force, Vus = 120 – 44.16 = 75.84 kN
If ‘s’ is the spacing of sheer reinforcementVs = d × 0.87 × fy × Ast xs Ast = 2 × π × 82 = 100.53 mm2 4 ∴ s = d × 0.87 fy Ast Vus = 400 × 0.87 × 250 × 100.53 = 115.323 mm 75.84 × 103
- In addition, the beam is subjected to a torque whose factored value is 10.90 kNm. The stirrups have to be provided to carry a shear (kN) equal to
-
View Hint View Answer Discuss in Forum
Equivalent SF = 1.6T b = 1.6 × 10.9 × 1000 = 75.82 kN 230
Total SF = 75.82 + 75.84 = 150.67 kNCorrect Option: C
Equivalent SF = 1.6T b = 1.6 × 10.9 × 1000 = 75.82 kN 230
Total SF = 75.82 + 75.84 = 150.67 kN
Direction: Assume straight line instead of parabola for stress-strain curve of concrete as follows and partial factor for safety as 1.0.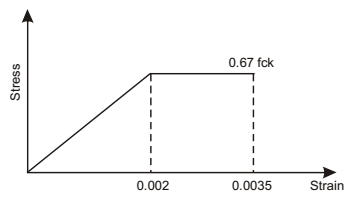
A rectangular under-reinforced concrete section of 300 mm width and 500 mm effective depth is reinforced with 3 bars of grade Fe G15, wach of 16 mm diameter. Concrete mix is M20.
- The depth of neutral axis from the compression fibre is
-
View Hint View Answer Discuss in Forum
Tension force = compression force
0.87 fy Ast = 0.67 fck (b.x2) + (1/2)0.67 fck(bx1)x = 0.0035 y 0.0020 ∴ x1 = 4 xu x2 = 3 xu 7 7 0.87 × 415 × 3 × π × 162 4
= 0.67 × 20 × 300 × (3/7) xu + (1/2) × 0.67 × 20 × 300 × (4/7) xu
∴ xu = 76 mmCorrect Option: A
Tension force = compression force
0.87 fy Ast = 0.67 fck (b.x2) + (1/2)0.67 fck(bx1)x = 0.0035 y 0.0020 ∴ x1 = 4 xu x2 = 3 xu 7 7 0.87 × 415 × 3 × π × 162 4
= 0.67 × 20 × 300 × (3/7) xu + (1/2) × 0.67 × 20 × 300 × (4/7) xu
∴ xu = 76 mm
- The depth of the neutral axis obtained as per IS: 456-2000 differs from the depth of neutral axis obtained in 26 (a) by
-
View Hint View Answer Discuss in Forum
Tension force = compression force
0.87 fy Ast = 0.30 fck = b.xu
0.87 × 415 × 3 × (π/4) × 162
= 0.36 × 20 × 300 × xu
∴ xu = 100.3 mm
Difference = 100.3 – 76 ≈ 25 mmCorrect Option: C
Tension force = compression force
0.87 fy Ast = 0.30 fck = b.xu
0.87 × 415 × 3 × (π/4) × 162
= 0.36 × 20 × 300 × xu
∴ xu = 100.3 mm
Difference = 100.3 – 76 ≈ 25 mm

