Surveying miscellaneous
- In the figure given below, lengths PQ(WCB : 30°) and QR (WCB : 45°) respectively up to three places of decimal are

-
View Hint View Answer Discuss in Forum
Let PQ = a, QR = b
Line PQ
Latitude = 100 + x1 cos 30°
Departure = 200 + x1 sin 30°
Line QR
Latitude = 1000 – x2 cos 45°
Departure = 1000 – x2 sin 45°
For closed traverse, 100 + x1 cos 30° = 1000 – x2 cos 45°
⇒ x1 cos 30° + x2 cos 45° = 900 200 + x1 sin 30° = 1000 – x2 sin 45°
⇒ x1 sin 30° + x2 sin 45° = 800
∴ x1 = 273.205 m , x2 = 938.186 cm.Correct Option: A
Let PQ = a, QR = b
Line PQ
Latitude = 100 + x1 cos 30°
Departure = 200 + x1 sin 30°
Line QR
Latitude = 1000 – x2 cos 45°
Departure = 1000 – x2 sin 45°
For closed traverse, 100 + x1 cos 30° = 1000 – x2 cos 45°
⇒ x1 cos 30° + x2 cos 45° = 900 200 + x1 sin 30° = 1000 – x2 sin 45°
⇒ x1 sin 30° + x2 sin 45° = 800
∴ x1 = 273.205 m , x2 = 938.186 cm.
- The following table gives data of consecutive co-ordinates in respect of a closed theodolite traverse PQRSP.
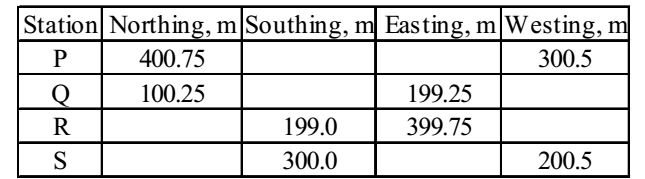
The magnitude and direction of error of closure in whole circle bearing are
-
View Hint View Answer Discuss in Forum
∑L = 400.75 + 100.25 – 199 – 300 = 2
∑D = – 300.5 + 199.25 + 399.75 – 200.5 = – 2
Error of closure = √(∑C)² + (∑D)² = √4 + 4 = 2√2tan θ = ∑D = - 1 ∑L
∴ θ = 315°
Correct Option: C
∑L = 400.75 + 100.25 – 199 – 300 = 2
∑D = – 300.5 + 199.25 + 399.75 – 200.5 = – 2
Error of closure = √(∑C)² + (∑D)² = √4 + 4 = 2√2tan θ = ∑D = - 1 ∑L
∴ θ = 315°
- The plan of a map was photo copied to a reduced size such that a line originally 100 mm, measures 90 mm. The original scale of the plan was 1 : 1000. The revised scale is
-
View Hint View Answer Discuss in Forum
Shrinkage factor = 90 = 0.9 100
Revised side = Original scale × reduction factor/ Shrinkage factor= 1 × 0.9 = 1 1000 1111.11 Correct Option: B
Shrinkage factor = 90 = 0.9 100
Revised side = Original scale × reduction factor/ Shrinkage factor= 1 × 0.9 = 1 1000 1111.11
- The following measurements were made during testing a levelling instrument.
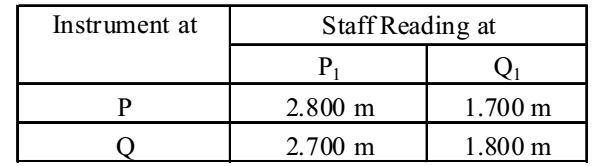
P1 is close to P and Q1 is close to Q. If the reduced level of station P is 100.000 m, the reduced level of station Q is
-
View Hint View Answer Discuss in Forum
Apparant diff. in elevation (from P) = 1.700 – 2.800 = – 1.1 m
Apparant diff. in elevation (from Q) = 1.800 – 2.700 = – 0.90 m∴ True difference = 1.1 + 0.9 = 1 m 2
∴ True elevation of Q = 100 + 1 = 101 mCorrect Option: C
Apparant diff. in elevation (from P) = 1.700 – 2.800 = – 1.1 m
Apparant diff. in elevation (from Q) = 1.800 – 2.700 = – 0.90 m∴ True difference = 1.1 + 0.9 = 1 m 2
∴ True elevation of Q = 100 + 1 = 101 m
- Consider the following figure, which is an extract from a contour map (scale = 1 : 20,000) of an area. An alignment of a road at a ruling gradient of 4% is to be fixed from the point O and beyond. What should be the radius of the arc with O as the centre to get the point of a alignment on the next contour on the map.

-
View Hint View Answer Discuss in Forum
Interval of contour = 20 m.
∴ length of arc = 20 = 500 m (4% gradient) 0.04 For 1 : 20,000 side, 500 m will be 500 on map i.e., 2.5 cm 20,000
Correct Option: C
Interval of contour = 20 m.
∴ length of arc = 20 = 500 m (4% gradient) 0.04 For 1 : 20,000 side, 500 m will be 500 on map i.e., 2.5 cm 20,000

