11. The three-dimensional state of stress at a point is given by
    
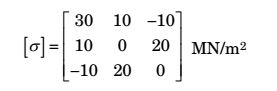
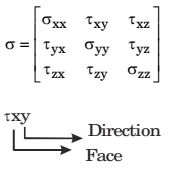
    The shear stress on the x-face in y-direction at the same point is then equal to
    

1. 1. zero MN/m²
      
      

   
   
   

   2. -10 MN/m²
      

   
   
   

   3. 10 MN/m²
      

   
   
   

   4. 20 MN/m²
      

   
   
   

---

1. View Hint View Answer Discuss in Forum

   

   Correct Option: C

   

---

12. A large uniform plate containing a rivet hole is subjected to uniform uniaxial tension of 95 MPa. The maximum stress in the plate is
    
    
    

1. 1. 100 MPa
      

   
   
   

   2. 285 MPa
      

   
   
   

   3. 190 MPa
      

   
   
   

   4. Indetermine

   
   
   

---

1. View Hint View Answer Discuss in Forum

   
   

   σ =	P
   	A

   
   P = σ A = 95 × 10⁶ × 10 × 10^–2 t
   

   σ =	P	=	95 × 106 × 10 × 10–2 t	= 190 MPa
   	A		(10 × 10-2 - 5 × 10–2)t

   Correct Option: B

   
   

   σ =	P
   	A

   
   P = σ A = 95 × 10⁶ × 10 × 10^–2 t
   

   σ =	P	=	95 × 106 × 10 × 10–2 t	= 190 MPa
   	A		(10 × 10-2 - 5 × 10–2)t

---

---

13. At a point in a stressed body the state of stress on two planes 45° apart is as shown below. Determine the two principal stresses in MPa.
    
    

1. 1. 8.242, 0.658
      

   
   
   

   2. 9.242, 0.758
      

   
   
   

   3. 9.242, 0.758
      

   
   
   

   4. 8.242, 0.758

   
   
   

---

1. View Hint View Answer Discuss in Forum

   
   σ_x = 8 MPa
   τ_xy = 3MPa
   σ_n = 2 MPa
   θ = 45°
   

   σn =	σx + σy	+	σx - σy	cos2θ - τxysin2θ
   	2		2

   
   

   2 =	8 + σy	+	8 - σy	(0) - 3sin(90)
   	2		2

   
   ( σ_y = 2 MPa )
   

   σ1 , 2 =	σx + σy	+ √			σx - σy		²	+ τ²xy
   	g				2

   
   

   =	8 + 2	± √			8 - 2		²	+ 32
   	2				2

   
   = 5 ± 4.242
   σ_{1 / 2} = 9.242, 0.758 MPa
   

   Correct Option: D

   
   σ_x = 8 MPa
   τ_xy = 3MPa
   σ_n = 2 MPa
   θ = 45°
   

   σn =	σx + σy	+	σx - σy	cos2θ - τxysin2θ
   	2		2

   
   

   2 =	8 + σy	+	8 - σy	(0) - 3sin(90)
   	2		2

   
   ( σ_y = 2 MPa )
   

   σ1 , 2 =	σx + σy	+ √			σx - σy		²	+ τ²xy
   	g				2

   
   

   =	8 + 2	± √			8 - 2		²	+ 32
   	2				2

   
   = 5 ± 4.242
   σ_{1 / 2} = 9.242, 0.758 MPa
   

---

14. A thin cylinder of 100 mm internal diameter and 5 mm thickness is subjected to an internal pressure of 10 MPa and a torque of 2000 Nm. Calculate the magnitudes of the principal stresses.
    

1. 1. 109.75 & 40.25 MPa

   
   
   

   2. 19.75 & 40.25 MPa

   
   
   

   3. 101.75 & 41.25 MPa

   
   
   

   4. 19.75 & 44.25 MPa

   
   
   

   5. None of these

   
   
   

---

1. View Hint View Answer Discuss in Forum

   d_i = o.1 m, d_o = di + 2t
   t = 0.005 m, d_o = 0.11 m
   T = 2000 Nm
   P = 10 MPa
   

   σc =	pdi	=	10 × 106 × 0.1	= 50 MPa
   	4t		4 × 0.005

   
   

   σc =	pdi	=	10 × 106 × 0.1	= 100 MPa
   	2t		2 × 0.005

   
   

   	T	=	τ
   	J		r

   
   

   τ =	Tr
   	J

   
   
   

   =	200 ×	0.11
   		2
   	π	(0.114 - 0.14)
   	32

   
   

   σ1 , 2 =	σx + σy	± √			σx - σy		²	+ τ²xy
   	2				2

   
   

   =	50 + 100	± √			50 - 100		²	+ 24.142
   	2				2

   
   = 75 ± 34.75
   = 109.75 & 40.25 MPa

   Correct Option: A

   d_i = o.1 m, d_o = di + 2t
   t = 0.005 m, d_o = 0.11 m
   T = 2000 Nm
   P = 10 MPa
   

   σc =	pdi	=	10 × 106 × 0.1	= 50 MPa
   	4t		4 × 0.005

   
   

   σc =	pdi	=	10 × 106 × 0.1	= 100 MPa
   	2t		2 × 0.005

   
   

   	T	=	τ
   	J		r

   
   

   τ =	Tr
   	J

   
   
   

   =	200 ×	0.11
   		2
   	π	(0.114 - 0.14)
   	32

   
   

   σ1 , 2 =	σx + σy	± √			σx - σy		²	+ τ²xy
   	2				2

   
   

   =	50 + 100	± √			50 - 100		²	+ 24.142
   	2				2

   
   = 75 ± 34.75
   = 109.75 & 40.25 MPa

---

---

15. A circular rod of diameter d and length 3d is subjected to a compressive force F acting at the top point as shown below. Calculate the stress at the bottom most support point A
    
    

1. 1. 	12F
      	πd2

      
      

   
   
   

   2. 	16F
      	πd2

      
      

   
   
   

   3. -	4F
      	πd2

      
      

   
   
   

   4. -	12F
      	πd2

   
   
   

---

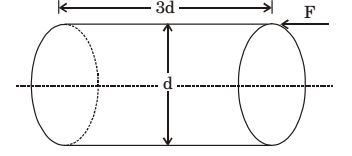
1. View Hint View Answer Discuss in Forum

   
   Stress due to Axial force
   

   σa =	F	=	F	=	4F	(compressive)
   	A		(π / 4)d2		πd2

   
   Stress due to bending:
   

   σb =	My	=	Fd	×	d	=	16F	(tensile)
   			2		2
   	I		π	d4			πd2
   			64

   
   Combined stress:
   σ_r = σ_a + σ_b
   

   σr =	-4F	+	16F	=	12F
   	πd2		πd2		πd2

   
   

   σr =	12F
   	πd2

   
   

   Correct Option: A

   
   Stress due to Axial force
   

   σa =	F	=	F	=	4F	(compressive)
   	A		(π / 4)d2		πd2

   
   Stress due to bending:
   

   σb =	My	=	Fd	×	d	=	16F	(tensile)
   			2		2
   	I		π	d4			πd2
   			64

   
   Combined stress:
   σ_r = σ_a + σ_b
   

   σr =	-4F	+	16F	=	12F
   	πd2		πd2		πd2

   
   

   σr =	12F
   	πd2

   
   

---