An ordered n-tuple (d1, d2,.., dn) with d1 ≥ d2 ≥

Home » Programming & Data Structure » Programming and data structure miscellaneous » Question

An ordered n-tuple (d₁, d₂,.., d_n) with d₁ ≥ d₂ ≥ ... ≥ d_n is called graphic if there exists a simple undirected graph with n vertices having degrees d₁ , d₂ ,..., d_n respectively. Which of the following 6-tuples is NOT graphic?

1. (1, 1, 1, 1, 1, 1)
2. (2, 2, 2, 2, 2, 2)
3. (3, 3, 3, 1, 0, 0)
4. (3, 2, 1, 1, 1, 0)

Correct Option: C

An ordered n type is graphic if it is a degree sequence of some simple undirected graph. options with corresponding graphs are shown below :–
(a) is Graphic seq. (1, 1, 1, 1, 1, 1)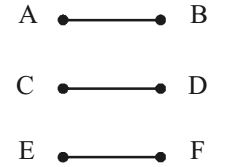

(b) is Graphic seq. (2, 2, 2, 2, 2, 2)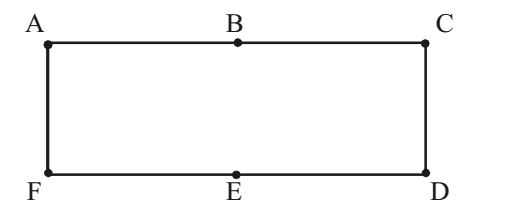

(d) is Graphic seq. (3, 2, 1, 1, 1, 0)

(c) is not graphic seq. (3, 3, 3, 1, 0, 0)
Clearly we can safely remove isolated vertices (i.e. vertices with zero degree) to prepare the graph with this degree sequence. Remaining sequence is (3, 3, 3, 1). Let us name these as A, B, C, D Now vertex with degree 1 (is D) Must be connect only one A, B or C. If we remove this also then 3 vertices remains A, B and C. One of them will have degree = 2 and other's degree = 3. Now remove vertex with degree 2, finally two vertices remains that must have degree = 2 which is not possible in a simple undirected graph. Hence the seq. (3, 3, 3, 1, 0, 0) is not graphic.