Correct Option: B

The vertices of Graphs are ordered pair (i, j) where two vertices (a, b) and (c, d) are connected by an edge only if |a – c| ≤ 1 and |b – d| ≤ 1. Also given that 1 ≤ i ≤ 12, i ≤ j ≤ 12.
So, for example (1, 2) is connected to (1, 1), (2, 1), (2, 2), (2, 3) and (1, 3)
Similarly (5, 5) is connected to (4, 4), (4, 5), (4, 6), (5, 4), (5, 6), (6, 4), (6, 5) and (6, 6) and (1, 12) is connected only to (1, 11), (2, 11) and (2, 12).
So, different vertices are connected to different number of vertices. However we can visualize this easily using following diagram :–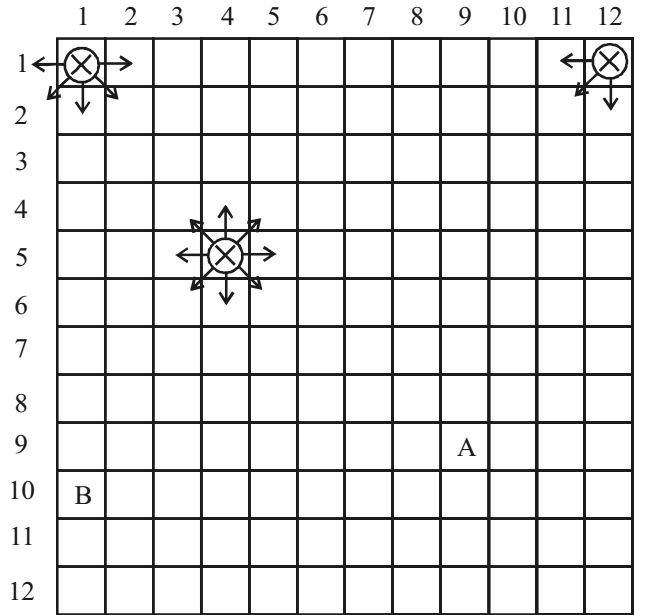

Each cell of the table represents corresponding vertex of the graph. For example the cell ‘A’ represents vertex (9, 0) of the graph, similarly ‘B’ represents vertex (10, 2) of the graph. Now, we easily see that there are three kind of vertices in the graph (or table) :
(i) Corner vertices which are connected to ‘3’ neighbours. No. of such vertices = 4
Total no. of edges for such vertices = 4 × 3 = 12
(ii) Vertices in first/ last row of first/last column except corner vertices, which are connected to ‘5’ neighbours each.
No. of such vertices = 40
Total no. of edges for such vertices = 40 × 5 = 200
(iii) Internal cells (vertices) that are connected to ‘8’ neighbours each.
No. of such vertices = 100
Total no. of edges for these vertices = 100 × 8 = 800
Edge total of all above cases = 12 + 200 + 800 = 1012
However in above calculation each edge is counted twice, so, finally total no. of edges in the graph