Let x(t) and y(t) (with Fourier transforms X(f) and Y(f)

Home » Signals and Systems » Signal and systems miscellaneous » Question

Let x(t) and y(t) (with Fourier transforms X(f) and Y(f) respectively) be related as shown in figure.

Then Y(f) is—

1. – 1 X f e^{– j2πf}
  2 2
2. – 1 X f e^j2πf
  2 2
3. – X f e^j2πf
  2
4. – X f e^{– j2πf}
  2

Correct Option: D

From fig. we see that y(t) is a compressed version of x(t). But in frequency domain it will be represented by expansion i.e., shifting of two unit left side.
First shifting then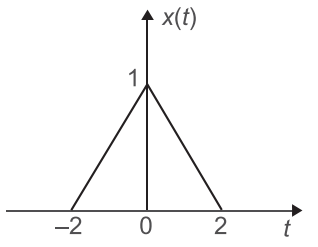

Scaling and then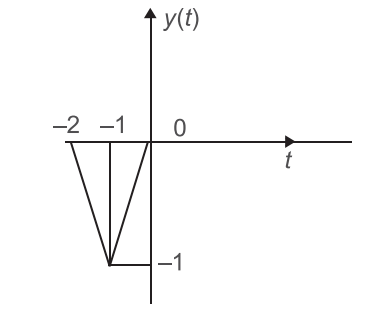

Amplitude reflection i.e.,
x(t) = – x(t)

we get – X		f		e^–j2πf
		2

–	1	X		f		e^{– j2πf}
	2			2

–	1	X		f		e^j2πf
	2			2

– X		f		e^j2πf
		2

– X		f		e^{– j2πf}
		2