-
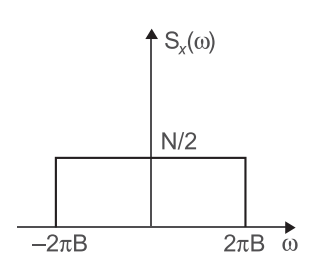
The power spectral density is shown below then Rx(τ) is—
-
- NB sin c (2πBτ)
-
1 sin c (2πBτ) NB - NB sin c (πBτ)
-
1 sin c (πBτ) NB
Correct Option: A
| Rxx(τ) = |  | ∞ | Sx(ω) ejωt .dω | 2π | 0 |
| Given that Sx(ω) = |  | ;|ω| = 2πB | |
| 2 | |||
| 0; otherwise | |||
| so, Rx(τ) = |  | 2πB | · ejωt dω | 2π | – 2πB | 2 |
| = |  |  | 2πB | ||||
| 4π | jτ | – 2πB |
| = |  |  | |||||
| 2πτ | 2τ |
| = | sin 2πBτ | 2πτ |
| = NB | 2πBτ {∵sin x/x = sinc x} | 2πτ |
= NB sinc (2πBτ)

