Oscillations Easy Questions and Answers | Page - 10

Oscillations

A particle, with restoring force proportional to displacement and resistve force proportional to velocity is subjected to a force F sin ω₀. If the amplitude of the particle is maximum for ω = ω₁ and the energy of the particle is maximum for ω = ω₂, then

1. ω₁ = ω₀ and ω₂ ≠ ω₀
1. ω₁ = ω₀ and ω₂ = ω₀
1. ω₁ ≠ ω₀ and ω₂ = ω₀
1. ω₁ ≠ ω₀ and ω₂ ≠ ω₀

View Hint View Answer Discuss in Forum

At maximum energy of the particle, velocity resonance takes place, which occurs when frequency of external periodic force is equal to natural frequency of undamped vibrations, i.e. ω₂ = ω₀.
Further, amplitude resonance takes place at a frequency of external force which is less than the frequency of undamped natural vibrations, i.e. . ω₁ ≠ ω₀ .

Correct Option: C

At maximum energy of the particle, velocity resonance takes place, which occurs when frequency of external periodic force is equal to natural frequency of undamped vibrations, i.e. ω₂ = ω₀.
Further, amplitude resonance takes place at a frequency of external force which is less than the frequency of undamped natural vibrations, i.e. . ω₁ ≠ ω₀ .

A body of mass M, executes vertical SHM with periods t₁ and t₂, when separately attached to spring A and spring B respectively. The period of SHM, when the body executes SHM, as shown in the figure is t₀. Then

1. t₀^–1 = t₁^–1 + t₂^–1
1. t₀ = t₁ + t₂
1. t₀² = t₁² + t₂²
1. t₀^–2 = t₁^–2 + t₂^–2

View Hint View Answer Discuss in Forum

t = 2π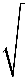
m
k

⇒ k = Const . t^-2
Here the springs are joined in parallel. So
k₀ = k₁ - k₂
where k₀ is resultant force constant
or , Const . t₀^-2 = Const . t₁^-2 + Const . t₂^-2
or , t₀² = t₁² + t₂²

Correct Option: D

t = 2π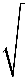
m
k

⇒ k = Const . t^-2
Here the springs are joined in parallel. So
k₀ = k₁ - k₂
where k₀ is resultant force constant
or , Const . t₀^-2 = Const . t₁^-2 + Const . t₂^-2
or , t₀² = t₁² + t₂²

The time period of a mass suspended from a spring is T. If the spring is cut into four equal parts and the same mass is suspended from one of the parts, then the new time period will be

1. 2T
1. T
  4
1. 2
1. T
  2

View Hint View Answer Discuss in Forum

T = 2π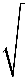
m
k

When a spring is cut into n parts Spring constant for each part = nk
Here, n = 4
∴ T₁ = 2π =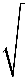
m T
4k 2

Correct Option: D

T = 2π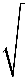
m
k

When a spring is cut into n parts Spring constant for each part = nk
Here, n = 4
∴ T₁ = 2π =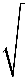
m T
4k 2

Two springs of spring constants k₁ and k₂ are joined in series. The effective spring constant of the combination is given by

1. k₁k₂ /(k₁ + k₂)
1. k₁k₂
1. (k₁ + k₂) /2
1. k₁ + k₂

View Hint View Answer Discuss in Forum

1 = 1 + 1 ⇒ 1 = k₁ + k₂
k_eq k₁ k₂ k_eq k₁ k₂

⇒ k_eq = k₁ k₂
k₁ + k₂

Correct Option: A

1 = 1 + 1 ⇒ 1 = k₁ + k₂
k_eq k₁ k₂ k_eq k₁ k₂

⇒ k_eq = k₁ k₂
k₁ + k₂

A particle executes simple harmonic oscillation with an amplitude a. The period of oscillation is T. The minimum time taken by the particle to travel half of the amplitude from the equilibrium position is

1. T/8
1. T/12
1. T/2
1. T/4

View Hint View Answer Discuss in Forum

Displacement from the mean position
y = a sin 2π t
T

According to problem y = a / 2
a / 2 = a sin 2π t
T

⇒ π = 2π t ⇒ t = T / 12
6 T

This is the minimum time taken by the particle to travel half of the amplitude from the equilibrium position.

Correct Option: B

Displacement from the mean position
y = a sin 2π t
T

According to problem y = a / 2
a / 2 = a sin 2π t
T

⇒ π = 2π t ⇒ t = T / 12
6 T

This is the minimum time taken by the particle to travel half of the amplitude from the equilibrium position.