System of Particles and Rotational Motion

System of Particles and Rotational Motion

Easy Questions
Moderate Questions
Difficult Questions

Mechanics

Physical World, Units and Measurements
Motion in a Straight Line
Motion in a Plane
Laws of Motion
Work, Energy and Power
Gravitation
Mechanical Properties of Solids
Mechanical Properties of Fluids
System of Particles and Rotational Motion
  1. A small mass attached to a string rotates on frictionless table top as shown. If the tension in the string is increased by pulling the string causing the radius of the circular motion to decrease by a factor of 2, the kinetic energy of the mass will








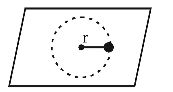
  1. View Hint View Answer Discuss in Forum

    K.E. = L²/2I
    The angular momentum L remains conserved about the centre.
    That is, L = constant.
    I = mr²
    ∴ K.E. = L²/2mr²
    In 2nd case,
    K.E. = L²/2(mr'²)
    But r′ = r/2

    ∴ K.E' =
    L²
    		 =
    4L²
    		 ⇒ K.E.′ = 4 K.E.
    MLω²
    22m.(r²/4)2mr²

    ∴ K.E. is increased by a factor of 4.

    Correct Option: C

    K.E. = L²/2I
    The angular momentum L remains conserved about the centre.
    That is, L = constant.
    I = mr²
    ∴ K.E. = L²/2mr²
    In 2nd case,
    K.E. = L²/2(mr'²)
    But r′ = r/2

    ∴ K.E' =
    L²
    		 =
    4L²
    		 ⇒ K.E.′ = 4 K.E.
    MLω²
    22m.(r²/4)2mr²

    ∴ K.E. is increased by a factor of 4.

  1. The moment of inertia of a thin uniform rod of mass M and length L about an axis passing through its midpoint and perpendicular to its length is I0. Its moment of inertia about an axis passing through one of its ends and perpendicular to its length is








  1. View Hint View Answer Discuss in Forum

    By theorem of parallel axes,
    I = Icm + Md²
    I = I0 + M (L/2)² = I0 + ML²/4

    Correct Option: B

    By theorem of parallel axes,
    I = Icm + Md²
    I = I0 + M (L/2)² = I0 + ML²/4

  1. The moment of inertia of a uniform circular disc is maximum about an axis perpendicular to the disc and passing through :








  1. View Hint View Answer Discuss in Forum

    According to parallel axis theorem of the moment of Inertia
    I = Icm + md²
    d is maximum for point B so Imax about B.

    Correct Option: A

    According to parallel axis theorem of the moment of Inertia
    I = Icm + md²
    d is maximum for point B so Imax about B.

  1. The ratio of radii of gyration of a circular ring and a circular disc, of the same mass and radius, about an axis passing through their centres and perpendicular to their planes are








  1. View Hint View Answer Discuss in Forum

    I = MK²
    ∴ K = √I/M
    Iring = MR² and Idisc = (1/2)MR²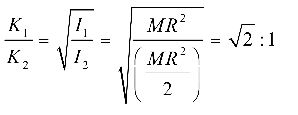


    Correct Option: A

    I = MK²
    ∴ K = √I/M
    Iring = MR² and Idisc = (1/2)MR²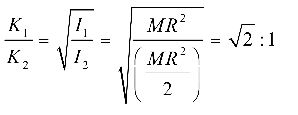


  1. Three identical spherical shells, each of mass m and radius r are placed as shown in figure. Consider an axis XX' which is touching to two shells and passing through diameter of third shell. Moment of inertia of the system consisting of these three spherical shells about XX' axis is









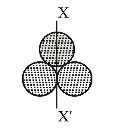
  1. View Hint View Answer Discuss in Forum

    Moment of inertia of shell 1 along diameter
    Idiameter = (2/3) MR²
    Moment of inertia of shell 2 = m. i of shell 3

    = Itangential =
    2
    		MR² + MR² =
    5
    		 MR²
    33

    So, I of the system along x x1
    = Idiameter + (Itangential) × 2
    or,
    = Itotal =
    2
    		MR² +
    5
    		 MR² × 2
    33

    =
    12
    		 MR² = 4MR²
    3

    Correct Option: C

    Moment of inertia of shell 1 along diameter
    Idiameter = (2/3) MR²
    Moment of inertia of shell 2 = m. i of shell 3

    = Itangential =
    2
    		MR² + MR² =
    5
    		 MR²
    33

    So, I of the system along x x1
    = Idiameter + (Itangential) × 2
    or,
    = Itotal =
    2
    		MR² +
    5
    		 MR² × 2
    33

    =
    12
    		 MR² = 4MR²
    3